Учебник. Тригонометрические неравенства

Нарисуем тригонометрическую окружность и отметим на ней точки, для которых ордината превосходит $\frac{1}{2}$

Для x ∈ [0; 2π] решением данного неравенства будут $x\in \left[\frac{\pi }{6}\mathrm{;}\frac{5\pi }{6}\right]\mathrm{.}$ Ясно также, что если некоторое число x будет отличаться от какого-нибудь числа из указанного интервала на 2πn, $n\in \mathbb{Z}$ то sin x также будет не меньше $\frac{1}{2}\mathrm{.}$ Следовательно, к концам найденного отрезка решения нужно просто добавить 2πn, где $n\in \mathbb{Z}$ Окончательно, получаем, что решениями исходного неравенства будут все $x\in \left[\frac{\pi }{6}+2\pi n\mathrm{;}\frac{5\pi }{6}+2\pi n\right]\mathrm{,}$ где $n\in \mathbb{Z}$

Ответ. $x\in \left[\frac{\pi }{6}+2\pi n\mathrm{;}\frac{5\pi }{6}+2\pi n\right]\mathrm{,}$ где $n\in \mathbb{Z}$

Обозначим $t=\pi +\frac{x}{3}$ тогда неравенство примет вид простейшего: tg t ≥ –1. Рассмотрим интервал $t\in \left(\mathrm{-}\frac{\pi }{2}\mathrm{;}\frac{\pi }{2}\right)$ длиной, равной наименьшему положительному периоду (НПП) тангенса. На этом отрезке с помощью линии тангенсов устанавливаем, что $t\in \left[\mathrm{-}\frac{\pi }{4}\mathrm{;}\frac{\pi }{2}\right)$ Вспоминаем теперь, что необходимо добавить πn, где $n\in \mathrm{\mathbb{Z},}$ поскольку НПП функции tg x T = π. Итак, $t\in \left[\mathrm{-}\frac{\pi }{4}+\pi n\mathrm{;}\frac{\pi }{2}+\pi n\right)$ Возвращаясь к переменной x, получаем, что $\begin{array}{l}\pi +\frac{x}{3}\in \left[\mathrm{-}\frac{\pi }{4}+\pi n\mathrm{;}\frac{\pi }{2}+\pi n\right)\iff \frac{x}{3}\in \left[\mathrm{-}\frac{\pi }{4}-\pi +\pi n\mathrm{;}\frac{\pi }{2}-\pi +\pi n\right)\iff \\ \iff \frac{x}{3}\in \left[\mathrm{-}\frac{5\pi }{4}+\pi n\mathrm{;}\mathrm{-}\frac{\pi }{2}+\pi n\right)\iff x\in \left[\mathrm{-}\frac{15\pi }{4}+3\pi n\mathrm{;}\mathrm{-}\frac{3\pi }{2}+3\pi n\right)\mathrm{.}\end{array}$

Ответ. $x\in \left[\mathrm{-}\frac{15\pi }{4}+3\pi n\mathrm{;}\mathrm{-}\frac{3\pi }{2}+3\pi n\right)\mathrm{,}\text{ где }n\in \mathbb{Z}$

Неравенства с обратными тригонометрическими функциями удобно решать с использованием графиков обратных тригонометрических функций. Покажем, как это делается на примере.

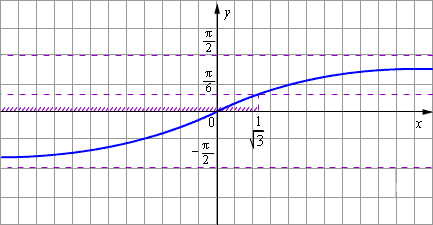
Нарисуем график функции y = arctg x. Найдём точку пересечения этого графика с горизонтальной прямой $y=\frac{\pi }{6}$ Это точка с абсциссой $x=\frac{1}{\sqrt{3}}$ По графику видно, что для всех $x\le \frac{1}{\sqrt{3}}$ график функции лежит ниже прямой $y=\frac{\pi }{6}$ Следовательно, эти x и составляют:

Ответ. $x\le \frac{1}{\sqrt{3}}$