Учебник. Основные понятия тригонометрии

В геометрии угол определяется как часть плоскости, ограниченная двумя лучами. При таком определении получаются углы от 0° до 180°. Однако угол можно рассматривать и как меру поворота. Возьмем на координатной плоскости окружность радиуса R с центром O в начале координат. Пусть одна сторона угла α с вершиной в начале координат O идёт по оси абсцисс, а сам угол положительный, то есть, по определению, отложен по направлению против часовой стрелки от положительного направления оси абсцисс. Из геометрии известно, что отношение длины дуги l, на которую опирается этот угол, к радиусу R этой окружности не зависит от самого радиуса. Поэтому это отношение может быть выбрано характеристикой и мерой данного угла: $\alpha =\frac{l}{R}$

Такая мера называется радианной мерой угла и используется наравне с угловой. Говорят, что угол равен определённому числу радиан. Ясно, что угол в один радиан опирается на длину дуги окружности, равную её радиусу. В самом деле: $\alpha =\frac{R}{R}=1$ Обозначение радиана – «рад». Так как длина всей окружности радиуса R равна 2πR, то всей окружности соответствует угол $\alpha =\frac{2\pi R}{R}=2\pi$ радиан. Поскольку вся окружность содержит 360°, то один радиан соответствует $\frac{{360}^{°}}{2\pi }=\frac{{180}^{°}}{\pi }$ градусов: $1\text{ рад}=\frac{{180}^{°}}{\pi }\approx {57}^{°}17^{\mathrm{\prime }}$

И наоборот, $1^{°}=\frac{\pi }{180}\text{ рад}$

Значит, можно написать следующие формулы перехода от градусного измерения к радианному: $\alpha =\frac{\pi {\alpha }^{°}}{{180}^{°}}\text{ рад}$

и от радианного измерения к градусному: ${\alpha }^{°}=\frac{{180}^{°}}{\pi }\alpha$

Обозначение «рад» при записи часто опускают и вместо, например, 180° = π рад пишут просто 180° = π.

Пользуясь этими формулами, легко получить следующую таблицу перевода некоторых наиболее часто встречающихся углов из градусной меры в радианную и обратно.

Угол, градусы	0°	30°	45°	60°	90°	180°	270°	360°
Угол, радианы	0	$\frac{\pi }{6}$	$\frac{\pi }{4}$	$\frac{\pi }{3}$	$\frac{\pi }{2}$	π	$\frac{3\pi }{2}$	2π

Определите радианную меру угла, если его градусная мера равна: 1) 2°; 2) 225°.

1) $\alpha =\frac{\pi }{180}ċ2=\frac{\pi }{90}$

2) $\alpha =\frac{\pi }{180}ċ225=\frac{5\pi }{4}$

Ответ. 1) $\frac{\pi }{90}$ 2) $\frac{5\pi }{4}$

Снова рассмотрим на координатной плоскости окружность радиуса R с центром O в начале координат. Как известно, координатные оси делят окружность на четыре дуги, которые называют четвертями.

Окружность радиуса R

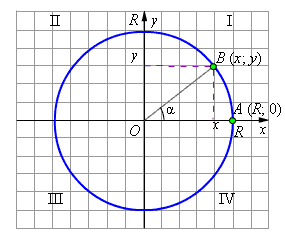
Рассмотрим произвольный угол α. Изобразим его как угол поворота радиус-вектора $\stackrel{⟶}{OA}$ против часовой стрелки. При таком повороте точка A (R; 0) перейдёт в некоторую точку B (x; y) на этой окружности, при этом $\angle AOB=\alpha$ (α может быть больше не только 180°, но и больше 360°). В зависимости от того, в какой четверти лежит точка B, угол α называется углом этой четверти.

Докажем, что отношения $\frac{x}{R}$ и $\frac{y}{R}$ не зависят от величины радиуса R. Действительно, выберем на отрезке OA точку $A_1$ такую, что $A_1\ne O$ Построим окружность с центром в начале координат радиуса $O{A}_1=R_1$ Построенная окружность пересекает радиус-вектор $\stackrel{⟶}{OB}$ в точке $B_1\mathrm{ (}{x}_1\mathrm{,}{y}_1\mathrm{)}$ Так как векторы $\stackrel{⟶}{OB}$ и $\stackrel{⟶}{O{B}_1}$ коллинеарны и одинаково направлены, то $\stackrel{⟶}{O{B}_1}=\lambda \stackrel{⟶}{OB}$

Однако равные векторы имеют равные координаты, следовательно, $x_1=\frac{R_1}{R}x$

Откуда следует после деления обеих частей последних равенств на R₁, что $\frac{x_1}{R_1}=\frac{x}{R}$

Итак, для любого угла поворота отношение координат радиус-вектора к его длине не зависит от этой длины радиус-вектора. Следовательно, отношения $\frac{x}{R}$ и $\frac{y}{R}$ характеризуют не окружность, а лишь угол поворота. Значит, для того, чтобы рассмотреть основные свойства этих отношений, можно взять окружность любого радиуса, например, R = 1. Так мы и сделаем. Окружность единичного радиуса с центром в начале координат называется тригонометрической окружностью.

Координатная окружность

Ввиду всего вышесказанного, рассмотренные отношения $\frac{x}{R}$ и пр. как характеристики только угла (но не окружности) удобно как-либо обозначить. Введём несколько ключевых определений.

Косинусом угла α называется абсцисса x точки B − конца радиус-вектора единичной окружности, образующего угол α с осью абсцисс. cos α = x.

Функция y = cos x

Синусом угла α называется ордината y точки B − конца радиус-вектора единичной окружности, образующего угол α с осью абсцисс. sin α = y.

Функция y = sin x

Тангенсом угла α называется отношение ординаты y к абсциссе x точки B − конца радиус-вектора единичной окружности, образующего угол α с осью абсцисс. $\text{tg }\alpha =\frac{y}{x}=\frac{\text{sin }\alpha }{\text{cos }\alpha }$

Функция y = tg x

Котангенсом угла α называется отношение абсциссы x к ординате y точки B − конца радиус-вектора единичной окружности, образующего угол α с осью абсцисс. $\text{ctg }\alpha =\frac{x}{y}=\frac{\text{cos }\alpha }{\text{sin }\alpha }$

Функция y = ctg x

Ясно, что для данного угла α функции sin α, cos α, tg α и ctg α, которые называются тригонометрическими функциями, определены однозначно (поскольку каждому углу соответствует единственная точка на тригонометрической окружности). Однако если функции sin α и cos α определены для любого угла α, то функции tg α и ctg α определены только для тех углов, для которых не равен нулю знаменатель дробей $\frac{x}{y}$ и $\frac{y}{x}$ Значит, tg α не определён для углов вида $\alpha =\frac{\pi }{2}+\pi k$ где $k\in \mathbb{Z}$  ctg α не определён для углов вида $\alpha =\pi k\text{, где }k\in \mathbb{Z}$

Поскольку синус по определению равен ординате точки на единичной окружности, а косинус − абсциссе, то знаки тригонометрических функций по четвертям будут такими:

Функция	Знаки тригонометрических функций по четвертям
	I	II	III	IV
sin α	+	+	−	−
cos α	+	−	−	+
tg α	+	−	+	−
ctg α	+	−	+	−

Вычисление тригонометрических функций некоторых углов

Вычисление углов

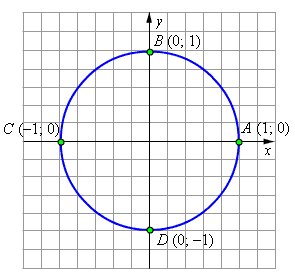
Найдём значения тригонометрических функций некоторых наиболее часто встречающихся углов. Конец радиус-вектора, отвечающего углу 0°, точка A, имеет координаты (1; 0). Поэтому cos 0° = 1, sin 0° = 0, tg 0° = 0, ctg 0° не определён. Совершенно аналогично рассматриваются точки B (0; 1), C (–1; 0) и D (0; –1), что даёт:

• sin 90° = 1, cos 90° = 0, ctg 90° = 0, tg 0° не определён.

• sin 180° = 0, cos 180° = –1, tg 180° = 0, ctg 180° не определён.

• sin 270° = –1, cos 270° = 0, ctg 270° = 0, tg 270° не определён.

Данные нами определения совпадают для острых углов с определениями тригонометрических функций в геометрии. В самом деле, например, синусом острого угла прямоугольного треугольника AOC (см. рис. 2.4.1.4) называлось отношение противолежащего катета к гипотенузе: $\text{sin }O=\frac{AC}{OA}$ Кроме того, в курсе геометрии было доказано, что значения тригонометрических функций острых углов не зависят от размеров прямоугольного треугольника.

Однако если мы поместим наш прямоугольный треугольник так, что его вершина – точка O – совпадёт с началом координат, а точка A будет лежать на единичной окружности (то есть мы выбираем тем самым гипотенузу OA = 1), то геометрическое определение синуса примет вид: $\text{sin }O=\frac{AC}{OA}=\frac{AC}{1}=AC$

Значит, синус острого угла равен ординате точки, лежащей на тригонометрической окружности. А это как раз совпадает с нашим определением синуса. Совершенно те же самые рассуждения приводят нас к полной эквивалентности геометрического определения тригонометрических функций с тем, что дано в настоящем разделе. Следовательно, для вычисления значений тригонометрических функций мы можем воспользоваться их геометрическим определением.

Прямоугольный треугольник

Правильный треугольник

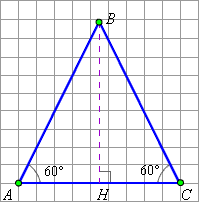
Рассмотрим правильный треугольник ABC со стороной, равной 1. Тогда по теореме Пифагора легко найти, что длина его высоты BH равна $BH=\sqrt{A{B}^2-A{H}^2}=\sqrt{1-{\left(\frac{1}{2}\right)}^2}=\frac{\sqrt{3}}{2}$

Прямоугольный равнобедренный треугольник

Значит, $\text{sin }{60}^{°}=\frac{BH}{AB}=\frac{\sqrt{3}}{2}\mathrm{,}\text{cos }{60}^{°}=\frac{AH}{AB}=\frac{1}{2}$ Рассматривая угол ABH, найдём, что $\text{sin }{30}^{°}=\frac{AH}{AB}=\frac{1}{2}\mathrm{,}\text{cos }{30}^{°}=\frac{BH}{AB}=\frac{\sqrt{3}}{2}$ Соответственно, $\text{tg }{\text{60}}^{°}=\frac{\text{sin }{60}^{°}}{\text{cos }{60}^{°}}=\sqrt{3}$ $\text{ctg }{60}^{°}=\frac{\text{cos }{60}^{°}}{\text{sin }{60}^{°}}=\frac{1}{\sqrt{3}}$ $\text{tg }{\text{30}}^{°}=\frac{\text{sin }{30}^{°}}{\text{cos }{30}^{°}}=\frac{1}{\sqrt{3}}$ $\text{ctg }{30}^{°}=\frac{\text{cos }{30}^{°}}{\text{sin }{30}^{°}}=\sqrt{3}$

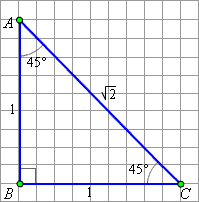
Рассмотрим теперь прямоугольный равнобедренный треугольник ABC с катетами, равными CA = CB = 1, ∠ CAB = 45°. Тогда по теореме Пифагора $AB=\sqrt{2}\mathrm{,}\angle CAB={45}^{°}$ и $\text{sin }{45}^{°}=\frac{CA}{AB}=\frac{1}{\sqrt{2}}=\text{cos }{45}^{°}$ Следовательно, $\text{tg }{45}^{°}=\text{ctg }{45}^{°}=1$

Итак, мы вычислили значения тригонометрических функций основных углов. Составим таблицу значений тригонометрических функций, которую мы только что получили.

Функция	Углы
	0°	30°	45°	60°	90°	180°	270°	360°	Градусы
	0°		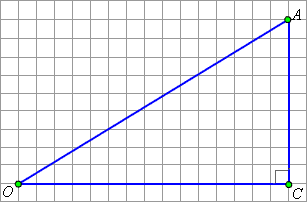						Радианы
sin α	0	$\frac{1}{2}$	$\frac{1}{\sqrt{2}}$	$\frac{\sqrt{3}}{2}$	1	0	–1	0
cos α	1	$\frac{\sqrt{3}}{2}$	$\frac{1}{\sqrt{2}}$	$\frac{1}{2}$	0	–1	0	1
tg α	0	$\frac{1}{\sqrt{3}}$	1	$\sqrt{3}$	–	0	–	0
ctg α	–	$\sqrt{3}$	1	$\frac{1}{\sqrt{3}}$	0	–	0	–

Найдите значения выражений

1) $\text{cos }{0}^{°}ċ\text{sin }{270}^{°}-\frac{2cos{180}^{°}}{{\text{cos}}^2{\mathrm{ 0}}^{°}}$

2) $\text{sin }\frac{\pi }{2}ċ{\text{cos}}^3\frac{\pi }{3}+\frac{1}{\text{cos }2\pi }+\frac{1}{\text{sin }\left(\frac{3\pi }{2}\right)}$

Имеем:

1) $\text{cos }{0}^{°}ċ\text{sin }{270}^{°}-\frac{2\text{cos }{180}^{°}}{{\text{cos}}^2{\mathrm{ 0}}^{°}}=1ċ\mathrm{(}\mathrm{-}1\mathrm{)}-\frac{2ċ\mathrm{(}\mathrm{-}1\mathrm{)}}{1^2}=\mathrm{-}1+2=1$

2) $\text{sin }\frac{\pi }{2}ċ{\text{cos}}^3\frac{\pi }{3}+\frac{1}{\text{cos }2\pi }+\frac{1}{\text{sin }\left(\frac{3\pi }{2}\right)}=1ċ{\left(\frac{1}{2}\right)}^3+\frac{1}{1}+\frac{1}{\mathrm{-}1}=\frac{1}{8}+1-1=\frac{1}{8}$

Ответ. 1) 1; 2) $\frac{1}{8}$

Периодические функции

Функция f называется периодической с периодом T ≠ 0, если для любого x из области определения функции выполнено: $\mathrm{f }\mathrm{(}x+T\mathrm{)}=\mathrm{f }\mathrm{(}x-T\mathrm{)}=\mathrm{f }\mathrm{(}x\mathrm{)}$

Если функция f имеет период T, то она, очевидно, имеет период nT, где $n\in \mathbb{Z}$ Поэтому говорят о наименьшем положительном периоде (НПП) функции f. Существуют периодические функции, не имеющие НПП. Так, например, f (x) = C, где C − произвольная постоянная, является периодической, однако любое положительное число является её периодом. Очевидно, среди них нет наименьшего.

Доказать, что НПП функции y = sin x является 2π.

Из определения функции следует, что у точек x и x + 2π одинаковая ордината, следовательно, sin x = sin (x + 2π), а это означает, что 2π является периодом функции sin x. Пусть T − некоторый период функции y = sin x. Тогда для всех x должно выполняться равенство sin x = sin (x + T). При x = 0 имеем sin T = 0. Значит, T может принимать значения только πn, где $n\in \mathbb{Z}$ Нас интересуют T < 2π. Таким периодом может быть только T = π, однако T = π не является периодом данной функции, так как равенство sin x = sin (x + π) неверно при $x=\frac{\pi }{2}$ Значит, НПП функции y = sin x является T = 2π.

Аналогично можно показать, что функция y = cos x также имеет НПП T = 2π. А функции y = tg x и y = ctg x имеют НПП T = π.