Открытая Математика. Алгебра. Степень с произвольным показателем

Степень с произвольным показателем

Пусть теперь $a \geq 0,$ $m, n \in ℕ, n \geq 2.$ По определению полагают, что $a^{\frac{m}{n}} = \sqrt[n]{a^{m}} .$ Если же a > 0, то по определению полагают, что $a^{- \frac{m}{n}} = \frac{1}{a^{\frac{m}{n}}} .$

Понятие нецелой степени отрицательного числа не имеет смысла.

Вычислить 1) $27^{\frac{1}{3}};$ 2) $81^{- \frac{3}{4}};$ 3) ${\frac{1}{16}}^{- \frac{1}{2}} .$

1) $27^{\frac{1}{3}} = \sqrt[3]{27} = 3;$

2) $81^{- \frac{3}{4}} = \frac{1}{81^{\frac{3}{4}}} = \frac{1}{\sqrt[4]{81^{3}}} = \frac{1}{\sqrt[4]{{(3^{4})}^{3}}} = \frac{1}{\sqrt[4]{3^{12}}} = \frac{1}{3^{3}} = \frac{1}{27};$

3) ${(\frac{1}{16})}^{- 1/2} = \frac{1}{{(\frac{1}{16})}^{1/2}} = \frac{1}{\sqrt{\frac{1}{16}}} = \frac{1}{\frac{1}{\sqrt{16}}} = \frac{1}{\frac{1}{4}} = 4.$

Ответ. 1) 3; 2) $\frac{1}{27};$ 3) 4.

Пусть a > 0, b > 0, r, s − любые рациональные числа. Тогда степень с любым рациональным показателем обладает следующими свойствами.

a^r ċ a^s = a^{r + s}.
a^r : a^s = a^{r – s}.
(a^r)^s = a^rs.
a^r ċ b^r = (ab)^r.
$\frac{a^{r}}{b^{r}} = {(\frac{a}{b})}^{r} .$

Упростите выражения 1) $8 x^{\frac{5}{6}} : 4 x^{- \frac{2}{3}};$ 2) $(x^{1/2} - y^{1/2}) (x^{1/2} + y^{1/2}) .$

1) $8 x^{\frac{5}{6}} : 4 x^{- \frac{2}{3}} = 2 x^{\frac{5}{6} - (- \frac{2}{3})} = 2 x^{\frac{5}{6} + \frac{2}{3}} = 2 x^{\frac{9}{6}} = 2 x^{\frac{3}{2}} .$

2) $(x^{1/2} - y^{1/2}) (x^{1/2} + y^{1/2}) = {(x^{1/2})}^{2} - {(y^{1/2})}^{2} = x - y .$

Ответ. 1) $2 x^{\frac{3}{2}};$ 2) x – y.

Итак, для любого действительного числа мы определили операцию возведения в натуральную степень; для любого числа $a \neq 0$ мы определили возведения в нулевую и целую отрицательную степень; для любого $a \geq 0$ мы определили операцию возведения в положительную дробную степень; для любого $a > 0$ мы определили операцию возведения в отрицательную дробную степень.

Возникает естественный вопрос: можно ли каким-либо образом определить операцию возведения в иррациональную степень, а, следовательно, определить смысл выражения a^x и для любого действительного числа x? Оказывается, что для положительных чисел a можно придать смысл записи a^α , где α − иррациональное число. Для этого нужно рассмотреть три случая: a = 1, a > 1, 0 < a < 1.

Если a = 1, то по определению полагают, что 1^α = 1.
Если a > 1, то выберем любое рациональное число r₁ < α и любое рациональное число r₂ > α. Тогда, очевидно, r₁ < r₂ и, следовательно: $\frac{a^{r_{1}}}{a^{r_{2}}} \overset{св-во 2}{====} a^{r_{1} - r_{2}} = \frac{1}{a^{r_{2} - r_{1}}} .$
Но $r_{2} - r_{1} > 0$ и потому (так как a > 1) $a^{r_{2}} - a^{r_{1}} > 1$ и, наконец, $\frac{a^{r_{1}}}{a^{r_{2}}} < 1 \Rightarrow a^{r_{1}} < a^{r_{2}} .$
Под $a^{α}$ понимают такое число, которое лежит между $a^{r_{1}}$ и $a^{r_{2}}$ при любом выборе чисел $r_{1}$ и $r_{2},$ обладающих свойством $r_{1} < α < r_{2} .$ Можно доказать, что число $a^{α}$ существует и единственно для любого a > 1 и любого иррационального α.
Если 0 < a < 1, то выберем любое рациональное число $r_{1} < α$ и любое рациональное число $r_{2} > α .$ Тогда, очевидно, $r_{1} < r_{2}$ и, следовательно, $a^{r_{1}} > a^{r_{2}}$ (это неравенство доказывается аналогично приведённому выше для a > 1). Под $a^{α}$ понимают такое число, которое лежит между $a^{r_{1}}$ и $a^{r_{2}}$ при любом выборе чисел $r_{1}$ и $r_{2},$ обладающих свойством $r_{1} < α < r_{2} .$ Можно доказать, что число $a^{α}$ существует и единственно для любого 0 < a < 1 и любого иррационального α.

Итак, для a > 0 мы определили степень с любым действительным показателем.

Пусть a > 0, b > 0, x и y − любые действительные числа. Тогда справедливы следующие свойства степени с любым действительным показателем:

a^x ċ a^y = a^{x + y}.
a^x : a^y = a^{x – y}.
(a^x)^y = a^xy.
a^x ċ b^x = (ab)^x.
$\frac{a^{x}}{b^{x}} = {(\frac{a}{b})}^{x} .$

Выше мы определили значение выражения a^b для всех вещественных a > 0 и всех вещественных b. Теперь мы можем определить степенную функцию.

Степенной функцией с вещественным показателем a называется функция y = x^a, x > 0.

Заметим, что для натуральных a степенная функция определена на всей числовой оси, подробнее об этом см. курс «Открытая Математика 2.6. Функции и Графики», § 2.4.2. Для произвольных вещественных a это невозможно, поэтому степенная функция с вещественным показателем определена только для положительных x.

К основным свойствам степенной функции y = x^a при a > 0 относятся:

Область определения функции − промежуток (0; +∞).
Область значений функции − промежуток (0; +∞).
Для любых a график функции проходит через точку (1; 1).
Функция строго монотонно возрастает на всей числовой прямой, то есть, если $x_{1} < x_{2},$ то $a^{x_{1}} < a^{x_{2}} .$
График степенной функции при a > 0 изображён на рисунке.

Степенная функция y = x^a при a > 0

Степенная функция y = x^a при a < 0

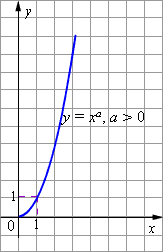
К основным свойствам степенной функции y = x^a при a < 0 относятся:

Область определения функции − промежуток (0; +∞).
Область значений функции − промежуток (0; +∞).
Для любых a график функции проходит через точку (1; 1).
Функция строго монотонно убывает на всей числовой прямой, то есть если $x_{1} < x_{2},$ то $a^{x_{1}} > a^{x_{2}} .$
График степенной функции при a < 0 изображён на рисунке.

Справедливы следующие свойства степенной функции:

$x^{a_{1}} x^{a_{2}} = x^{a_{1} + a_{2}} .$
$x^{a_{1}} : x^{a_{2}} = x^{a_{1} - a_{2}} .$
${(x^{a_{1}})}^{a_{2}} = x^{a_{1} a_{2}},$ если n > k.
$x^{a_{1}} > x^{a_{2}}$ на участке x > 1, если $a_{1} > a_{2} .$
$x^{a_{1}} < x^{a_{2}}$ на участке 0 < x < 1, если $a_{1} > a_{2} .$

Смотрите также: Математика, Английский язык, Химия, Биология, Физика, География, Астрономия.
А также: библиотека ЭОРов и образовательный онлайн-сервис с тысячами интерактивных работ "Облако знаний".

Учебник. Степень с произвольным показателем

ГЛАВНАЯ

НОВОСТИ

УЧЕБНИК

ДОСТУП К БЕСПЛАТНЫМ УРОКАМ