Открытая Математика. Алгебра. Корни многочлена

Корни многочлена

Как мы видели выше, методом выделения полного квадрата можно найти корни квадратного трехчлена. В случае многочленов высших степеней найти корни становится гораздо труднее, а иногда и просто невозможно. Попробуем это сделать там, где это достаточно просто.

Рассмотрим многочлен $P_{n} (x) = a_{n} x^{n} + a_{n - 1} x^{n - 1} + ... + a_{1} x + a_{0},$ где a₁, a₂, ..., a_n − целые числа, a_n ≠ 0.

Если многочлен $P_{n} (x) = a_{n} x^{n} + a_{n - 1} x^{n - 1} + ... + a_{1} x + a_{0}$ с целыми коэффициентами имеет рациональный корень $x_{0} = \frac{p}{q},$ то число p является делителем числа $a_{0}$ (свободного члена), а число q является делителем числа $a_{n}$ (старшего коэффициента).

Действительно, если число $x_{0} = \frac{p}{q}$ является корнем многочлена $P_{n} (x),$ то $P_{n} (\frac{p}{q}) = 0,$ а именно: $a_{n} {(\frac{p}{q})}^{n} + a_{n - 1} {(\frac{p}{q})}^{n - 1} + ... + a_{1} (\frac{p}{q}) + a_{0} = 0.$ Умножим обе части этого уравнения на $q^{n},$ получим: $\begin{array}{l} a_{n} p^{n} + a_{n - 1} p^{n - 1} q + a_{n - 1} p^{n - 2} q^{2} + ... + a_{1} p q^{n - 1} + a_{0} q^{n} = 0 \Leftrightarrow \\ \Leftrightarrow a_{n} p^{n} = - q (a_{n - 1} p^{n - 1} + a_{n - 1} p^{n - 2} q + ... + a_{1} p q^{n - 2} + a_{0} q^{n - 1}) . \end{array}$ Так как $a_{n}, a_{n - 1}, ..., a_{0}$ − целые числа, то в скобке стоит целое число. Значит, вся правая часть этого равенства делится на q, так как q входит в неё в качестве сомножителя. А значит и левая часть тождества делится на q, так как она равна правой. Число p не делится на q, так как иначе дробь $\frac{p}{q}$ была бы сократимой, значит и $p^{n}$ не делится на q. Следовательно, на q делится единственный из оставшихся сомножителей левой части, а именно $a_{n} .$ Аналогично доказывается, что $a_{0}$ делится на p. Теорема доказана.

Замечание. Эта теорема фактически позволяет находить корни многочленов высших степеней в том случае, когда коэффициенты этих многочленов − целые числа, а корень − рациональное число. Теорему можно переформулировать так: если нам известно, что коэффициенты многочлена − целые числа, а корни его − рациональны, то эти рациональные корни могут быть только вида $x_{0} = \frac{p}{q},$ где p является делителем числа $a_{0}$ (свободного члена), а число q является делителем числа $a_{n}$ (старшего коэффициента).

Пусть все коэффициенты многочлена $P_{n} (x) = a_{n} x^{n} + a_{n - 1} x^{n - 1} + ... + a_{1} x + a_{0}$ являются целыми числами, и пусть целое число a является корнем этого многочлена. Так как в этом случае $P_{n} (a) = 0 \Leftrightarrow a_{0} = - a (a_{n} a^{n - 1} + a_{n - 1} a^{n - 2} + ... + a_{1}),$ то отсюда следует, что коэффициент $a_{0}$ делится на a.

Разложить на множители многочлен x³ – 5x² – 2x + 16.

Данный многочлен имеет целые коэффициенты. Если целое число является корнем этого многочлена, то оно является делителем числа 16. Таким образом, если у данного многочлена есть целые корни, то это могут быть только числа ±1; ±2; ±4; ±8; ±16. Непосредственной проверкой убеждаемся, что число 2 является корнем этого многочлена, то есть x³ – 5x² – 2x + 16 = (x – 2)Q(x), где Q(x) − многочлен второй степени. Следовательно, многочлен разлагается на множители, один из которых (x – 2). Для поиска вида многочлена Q(x) воспользуемся так называемой схемой Горнера. Основным преимуществом этого метода является компактность записи и возможность быстрого деления многочлена на двучлен. По сути, схема Горнера является другой формой записи метода группировки, хотя, в отличие от последнего, является совершенно ненаглядной. Ответ (разложение на множители) тут получается сам собой, и мы не видим самого процесса его получения. Мы не будем заниматься строгим обоснованием схемы Горнера, а лишь покажем, как она работает.

1 −5 −2 16

2 1 −3 −8 0

В прямоугольную таблицу 2 × (n + 2) , где n − степень многочлена, (см. рис.) в верхнюю строчку выписываются подряд коэффициенты многочлена (левый верхний угол при этом оставляют свободным). В нижний левый угол записывают число − корень многочлена (или число x₀, если мы хотим разделить на двучлен (x – x₀)), в нашем примере это число 2. Далее вся нижняя строчка таблицы заполняется по следующему правилу.

Во вторую клетку нижней строки «сносится» число из клетки над ней, то есть 1. Затем поступают так. Корень уравнения (число 2) умножают на последнее написанное число (1) и складывают результат с числом, которое стоит в верхнем ряду над следующей свободной клеткой, в нашем примере имеем: 2 ċ 1 + (–5) = –3. Результат записывается в свободную клетку под тем числом, с которым только что производилось сложение, то есть под −5.

Далее корень 2 умножается на последнюю написанную цифру, то есть на −3, и складывается с числом, которое стоит в верхнем ряду над следующей свободной клеткой, то есть −2; имеем: 2 ċ (–3) + (–2) = –8. Результат пишем в свободную клетку под −2. Далее поступаем аналогично: 2 ċ (–8) + 16 = 0. В последней клетке (правый нижний угол), если нигде не совершено ошибки и 2 − действительно корень данного многочлена, должен получиться нуль. Это признак правильного решения. В общем случае в этой клетке оказывается остаток от деления исходного многочлена на (x – 2) (в нашем примере). У нас получился 0, следовательно, 2 − действительно корень этого многочлена.

Полученные числа 1, −3, −8 являются коэффициентами многочлена, который получается при делении исходного многочлена на x – 2. Значит, результат деления: 1 ċ x² + (–3)x + (–8) = x² – 3x – 8. Степень многочлена, полученного в результате деления, всегда на 1 меньше, чем степень исходного. Итак: x³ – 5x² – 2x + 16 = (x – 2)(x² – 3x – 8). Корни многочлена второй степени ищутся легко уже описанным выше способом (по формуле корней) и равны: $x_{1} = \frac{3 + \sqrt{41}}{2}$ и $x_{2} = \frac{3 - \sqrt{41}}{2} .$ Окончательно: $x^{3} - 5 x^{2} - 2 x + 16 = (x - 2) (x - \frac{3 - \sqrt{41}}{2}) (x - \frac{3 + \sqrt{41}}{2}) .$

Ответ. $(x - 2) (x - \frac{3 - \sqrt{41}}{2}) (x - \frac{3 + \sqrt{41}}{2}) .$

Разложить на множители многочлен x⁴ + 5x³ – 7x² – 5x + 6.

Данный многочлен имеет целые коэффициенты. Следовательно, если целое число является корнем этого многочлена, оно является делителем свободного члена, то есть числа 6. Таким образом, если у данного многочлена существуют целые корни, то это могут быть числа ±1; ±2; ±3; ±6.

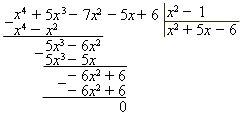
Проверкой убеждаемся, что числа +1 и −1 являются корнями многочлена, таким образом: x⁴ + 5x³ – 7x² – 5x + 6 = (x + 1)(x – 1)Q (x) = (x² – 1)Q (x), где Q (x) − многочлен второй степени. Делим исходный многочлен на x² – 1 уголком:

Итак: x⁴ + 5x³ – 7x² – 5x + 6 = (x² – 1)(x² + 5x – 6). По схеме Горнера нужно было бы выполнять два деления: на +1 и на −1, хотя, безусловно, при определённом навыке деление осуществляется с одинаковыми затратами времени, и какой метод избрать при делении − дело вкуса. Поэтому можно пользоваться всегда каким-то одним, наиболее понравившимся методом.

Говорят, что многочлен P (x) делится на двучлен (x – a), где a − задано, если P (x) можно представить в виде P (x) = Q (x)(x – a) + r, где Q (x) − многочлен степени на 1 меньше, чем P (x), а r − некоторое число, которое называется остатком от деления многочлена P (x) на (x – a). Если r = 0, то говорят, что многочлен P (x) делится на x – a без остатка.

Остаток от деления многочлена P (x) на двучлен (x – a) равен P (a), то есть P (x) = Q (x)(x – a) + P (a).

Число a является корнем многочлена P (x) тогда и только тогда, когда этот многочлен делится на (x – a) без остатка: P (x) = Q (x)(x – a), где Q (x) – многочлен степени, на 1 меньшей, чем P (x).

Необходимость. Если x = a − корень многочлена P (x), то по определению корня имеем P (a) = 0. По определению остатка имеем P (x) = Q (x)(x – a) + r, что при x = a имеет вид P (a) = r, но P (a) = 0, следовательно, r = 0, а значит, P (x) = Q (x)(x – a) + r = Q (x)(x – a), то есть справедливо нужное представление.

Достаточность. Пусть P (x) = Q (x)(x – a), тогда непосредственной подстановкой убеждаемся, что P (a) = 0, что значит, что x = a − корень многочлена P (x). Теорема доказана.

Смотрите также: Математика, Английский язык, Химия, Биология, Физика, География, Астрономия.
А также: библиотека ЭОРов и образовательный онлайн-сервис с тысячами интерактивных работ "Облако знаний".

Учебник. Корни многочлена

ГЛАВНАЯ

НОВОСТИ

УЧЕБНИК

ДОСТУП К БЕСПЛАТНЫМ УРОКАМ