Учебник. Операции над комплексными числами

Арифметические операции над комплексными числами были определены в предыдущем пункте. Эти операции обладают следующими свойствами:

1. Коммутативность сложения: z₁ + z₂ = z₂ + z₁ для любых $z_1\mathrm{, }{z}_2$ ∈ ℂ.
2. Ассоциативность сложения: (z₁ + z₂) + z₃ = z₁ + (z₂ + z₃) для любых $z_1\mathrm{,}{z}_2\in$ ℂ.
3. Существует такое число z = 0, которое обладает свойством z + 0 = z для любого z ∈ ℂ.
4. Для любых двух чисел z₁ и z₂ существует такое число z, что z₁ + z = z₂. Такое число z называется разностью двух комплексных чисел и обозначается z = z₂ – z₁.
5. Коммутативность умножения: z₁z₂ = z₂z₁ для любых $z_1\mathrm{, }{z}_2$ ∈ ℂ.
6. Ассоциативность умножения: (z₁z₂)z₃ = z₁(z₂z₃) для любых $z_1\mathrm{, }{z}_2\mathrm{, }{z}_3$ ∈ ℂ.
7. Дистрибутивность сложения относительно умножения: z₁(z₂ + z₃) = z₁z₂ + z₁z₃ для любых $z_1\mathrm{, }{z}_2\mathrm{, }{z}_3$ ∈ ℂ.
8. Для любого комплексного числа z: z ċ 1 = z.
9. Для любых двух чисел $z_1$ и $z_2$ существует такое число z, что $z_1ċz=z_2$ Такое число z называется частным двух комплексных чисел и обозначается $z=\frac{z_2}{z_1}\mathrm{.}$ Деление на 0 невозможно.

Все указанные свойства доказываются с помощью определения операций сложения и умножения.

Комплексно сопряжённые числа

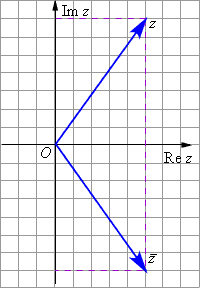
Комплексно сопряжённое число обозначается $\overline{z}$ Для этого числа справедливы соотношения: $\mathrm{|}z\mathrm{|}=\mathrm{|}\stackrel{\¯}{z}\mathrm{|}=\sqrt{a^2+b^2}\mathrm{;}$ $z\stackrel{\¯}{z}=\left(a+bi\right)\left(a-bi\right)=a^2+b^2={\mathrm{|}z\mathrm{|}}^2={\mathrm{|}\stackrel{\¯}{z}\mathrm{|}}^2$ $\frac{z_1}{z_2}=\frac{z_1{\stackrel{\¯}{z}}_2}{z_2{\stackrel{\¯}{z}}_2}=\frac{z_1{\stackrel{\¯}{z}}_2}{{\mathrm{|}{z}_2\mathrm{|}}^2}\mathrm{,}{z}_2\ne 0.$ Заметим, что последнее соотношение сводит операцию деления комплексных чисел к умножению $z_1\text{ на }{\overline{z}}_2$ и последующему делению на действительное число ${\mathrm{|}{z}_2\mathrm{|}}^2$