
Учебник. Векторы в пространстве
Вектор – направленный отрезок. Другими словами, вектором называется отрезок, для которого указано, какой из его концов является началом, а
На рисунках направление вектора обозначается стрелкой от начала к концу. Если длина рассматриваемого отрезка равна нулю, то есть отрезок вырождается в точку, то эта точка тоже может рассматриваться как вектор. Такой вектор называется нулевым и имеет произвольное направление.
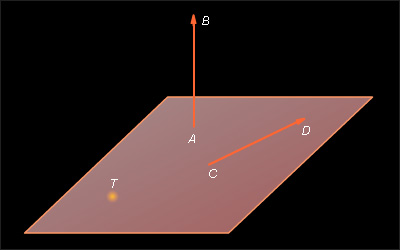
На рисунке 9.1.1 изображены ненулевые векторы и и нулевой вектор Нулевой вектор иногда обозначается символом
Длиной (модулем) ненулевого вектора называется длина отрезка AB. Она обозначается как Длина нулевого вектора равна нулю:
Два ненулевых вектора называются коллинеарными, если они лежат на одной прямой или на параллельных прямых.
Поскольку нулевой вектор может иметь произвольное направление, то разумно считать его коллинеарным любому ненулевому вектору.
Если два ненулевых вектора и коллинеарны, а лучи AB и CD сонаправлены, то векторы и называются сонаправленными. Этот факт обозначается так: Если же эти лучи не являются сонаправленными, то векторы и называются противонаправленными. Этот факт обозначается так:
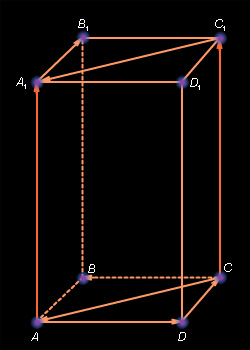
На рисунке 9.1.2
Два вектора называются равными, если они сонаправлены и их длины равны.
На рисунке 9.1.2 так как и а так как
Нетрудно доказать следующее.
От любой точки пространства можно отложить вектор, равный данному, и притом только один.
Сделайте это самостоятельно.
Два вектора называются противоположными, если их длины равны, и они противоположно
Суммой двух векторов и называется новый вектор который обозначается и получается следующим образом.
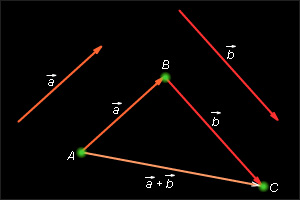
Отложим от произвольной точки A вектор , равный Теперь от точки B отложим вектор равный Вектор и называется суммой векторов и
Это правило сложения векторов называется правилом треугольника.
Для сложения двух неколлинеарных векторов можно воспользоваться правилом параллелограмма, известным из курса
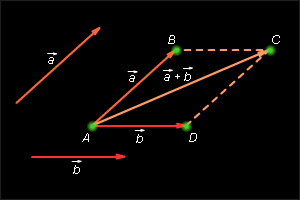
Для любых векторов и справедливы равенства:
- (переместительный закон);
- (сочетательный закон).
Разностью векторов и называется такой вектор сумма которого с вектором равна вектору
Обозначается разность векторов так:
где – вектор, противоположный вектору
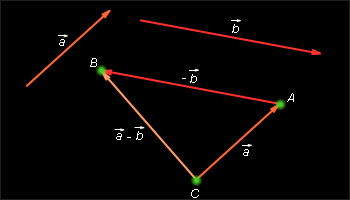
Сумма нескольких векторов не зависит от того, в каком порядке они складываются.
Доказательство этого утверждения следует из закона сложения векторов.
Произведением ненулевого вектора на число k называется вектор длина которого равна причём при k > 0 векторы и сонаправлены,
Из этого определения следует, что векторы и коллинеарны. Кроме того, произведение любого вектора на число 0 есть
Для любых векторов и любых
- (сочетательный закон);
- (первый распределительный закон);
- (второй распределительный закон).
Для коллинеарности вектора ненулевому вектору необходимо и достаточно, чтобы существовало такое
Эта теорема доказывается аналогично, как в планиметрии.
Для того, чтобы точка C лежала на прямой AB, необходимо и достаточно, чтобы существовало такое
Для параллельности прямых AM и BN необходимо и достаточно, чтобы существовало такое число λ, что
А также: библиотека ЭОРов и образовательный онлайн-сервис с тысячами интерактивных работ "Облако знаний".