Учебник. Правильный тетраэдр

Применение формул последнего параграфа к правильному тетраэдру позволяет получить ряд интересных соотношений для последнего. В этом параграфе мы приведём полученные формулы для данного конкретного случая и, кроме того, найдем выражения для некоторых характеристик правильного тетраэдра, таких как, например, объём, площадь полной поверхности и т. п.

Следуя обозначениям предыдущего параграфа, рассмотрим правильный тетраэдр SA₁A₂A₃ с длиной ребра a. Обозначения для его углов оставим теми же и вычислим их.

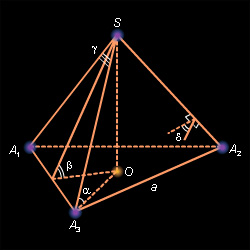
В правильном треугольнике $A_1$ длина высоты равна $A_{3}B=a\frac{\sqrt{3}}{2}\mathrm{.}$ Так как этот треугольник является правильным, то его высота одновременно является биссектрисой и медианой. Медианы, как известно, точкой своего пересечения делятся в отношении 2 : 1, считая от вершины. Несложно найти и точку пересечения медиан. Так как тетраэдр правильный, то этой точкой будет точка O – центр правильного треугольника $A_1$ Основание высоты правильного тетраэдра, опущенной из точки S, также проектируется в точку O. Значит, $B$ В правильном треугольнике $S$ длина апофемы тетраэдра равна $SB=a\frac{\sqrt{3}}{2}\mathrm{.}$ Применим теорему Пифагора для Δ SBO:

$S{O}^2=S{B}^2-B{O}^2\mathrm{.}$

Отсюда

$S{O}^2={\left(a\frac{\sqrt{3}}{2}\right)}^2-{\left(\frac{a}{2\sqrt{3}}\right)}^2=a^2\left(\frac{3}{4}-\frac{1}{12}\right)=\frac{2}{3}{a}^2\mathrm{.}$

Таким образом, высота правильного тетраэдра равна

$SO=a\sqrt{\frac{2}{3}}\mathrm{.}$

Площадь правильного треугольника – основания тетраэдра –

$S_{A_1{A}_2{A}_3}=\frac{\sqrt{3}}{4}{a}^2\mathrm{.}$

Значит, объём правильного тетраэдра равен

$V=\frac{1}{3}{S}_{A_1{A}_2{A}_3}\cdot SO=\frac{1}{3}\cdot \frac{\sqrt{3}}{4}{a}^2\cdot a\sqrt{\frac{2}{3}}=\frac{a^3\sqrt{2}}{12}\mathrm{.}$

$V=\frac{a^3\sqrt{2}}{12}\mathrm{.}$

Площадь полной поверхности тетраэдра в четыре раза больше площади его основания:

$S_{\mathrm{полн}}=a^2\sqrt{3}\mathrm{.}$

Двугранный угол при боковой грани для правильного тетраэдра, очевидно, равен углу наклона боковой грани к плоскости основания:

$cos\delta =cos\beta =\frac{BO}{BS}=\frac{a\frac{1}{2\sqrt{3}}}{a\frac{\sqrt{3}}{2}}=\frac{1}{3}\mathrm{.}$

$cos\delta =cos\beta =\frac{1}{3}\mathrm{;}$

$sin\delta =sin\beta =\frac{2\sqrt{2}}{3}\mathrm{.}$

Плоский угол при вершине правильного тетраэдра равен $\gamma ={60}^{\mathrm{○}}\mathrm{.}$

Угол наклона бокового ребра к плоскости основания можно найти из $\mathrm{\Delta }$  

$sin\alpha =\frac{SO}{S{A}_2}=\sqrt{\frac{2}{3}}\mathrm{.}$

$sin\alpha =\sqrt{\frac{2}{3}}\mathrm{;}$

$cos\alpha =\frac{1}{\sqrt{3}}\mathrm{;}$

$tg\alpha =\sqrt{2}\mathrm{.}$

Радиус вписанной сферы для правильного тетраэдра можно найти по известной формуле

$r=\frac{3V}{S_{\mathrm{полн}}}\mathrm{,}$

связывающей его с объёмом и площадью полной поверхности тетраэдра (отметим, что последняя формула справедлива для любого многогранника, в который можно вписать сферу). В нашем случае имеем

$r=\frac{3a^3\frac{\sqrt{2}}{12}}{a^2\sqrt{3}}=\frac{a}{2\sqrt{6}}\mathrm{:}$

$r=\frac{a}{2\sqrt{6}}\mathrm{.}$

Найдём радиус описанной сферы. Центр сферы, описанной около правильного тетраэдра, лежит на его высоте, так как именно прямая SO перпендикулярна плоскости основания и проходит через его центр, а на этой прямой должна лежать точка, равноудаленная от всех вершин основания тетраэдра. Пусть это точка $O_1$

тогда

$O_{1}S=O_1{A}_2=R\mathrm{.}$

Имеем

$O{O}_1=a\sqrt{\frac{2}{3}}-R\mathrm{.}$

Применим теорему Пифагора к треугольникам $B$ и $B$

$R^2=A_2{O}_1^2=B{A}_2^2+B{O}_1^2={\left(\frac{a}{2}\right)}^2+B{O}^2+O{O}_1^2={\left(\frac{a}{2}\right)}^2+{\left(\frac{a}{2\sqrt{3}}\right)}^2+{\left(a\sqrt{\frac{2}{3}}-R\right)}^2\mathrm{,}$

$R^2={\left(\frac{a}{2}\right)}^2+{\left(\frac{a}{2\sqrt{3}}\right)}^2+{\left(a\sqrt{\frac{2}{3}}-R\right)}^2=\frac{a^2}{4}+\frac{a^2}{12}+\frac{2}{3}{a}^2-2aR\sqrt{\frac{2}{3}}+R^2\mathrm{,}$

$2aR\sqrt{\frac{2}{3}}=a^2\left(\frac{1}{4}+\frac{1}{12}+\frac{2}{3}\right)=a^2\Rightarrow R=\frac{a\sqrt{6}}{4}\mathrm{,}$

$R=\frac{a\sqrt{6}}{4}\mathrm{.}$

Отметим, что

R = 3r,

r + R = H.

Если $H=SO=a\sqrt{\frac{2}{3}}\mathrm{,}$ то $r$

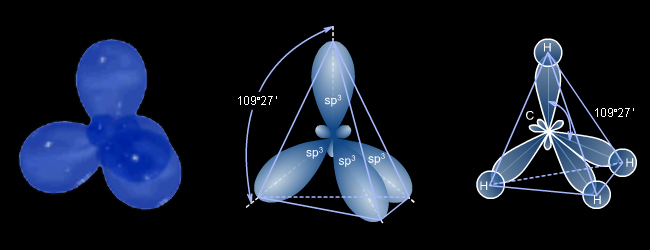
Интересно вычислить $\angle$ то есть тот угол, под которым видно ребро правильного тетраэдра из центра описанной сферы. Найдём его:

$\sin \angle B{O}_1{A}_2=\frac{B{A}_2}{O_1{A}_2}=\frac{\frac{a}{2}}{a\frac{\sqrt{6}}{4}}=\sqrt{\frac{2}{3}}\mathrm{,}$

$\cos \angle A_1{O}_1{A}_2=1-2{\mathrm{ sin}}^2 \angle B{O}_1{A}_2=1-2\cdot \frac{2}{3}=-\frac{1}{3}\mathrm{.}$

Значит,

$\angle A_1{O}_1{A}_2=arccos\left(\mathrm{-}\frac{1}{3}\right)\approx {109}^{○}28\mathrm{\text{'}}\mathrm{.}$

Это знакомая нам величина из курса химии: это угол между связями С–Н в молекуле метана, который удается очень точно измерить в эксперименте, а поскольку ни один атом водорода в молекуле СН₄, очевидно, ничем не выделен, то разумно предположить, что эта молекула имеет форму правильного тетраэдра. Этот факт подтверждается фотографиями молекулы метана, полученными при помощи электронного микроскопа.