Открытая Математика. Стереометрия. Объем частей шара

Объём частей шара

Шаровым сегментом называется часть шара, отсечённая от него плоскостью. Если OP – радиус шара, перпендикулярый отсекающей плоскости, то точку P назовём в этом случае полюсом шара. Высотой шарового сегмента называется отрезок PO₁, соединяющий полюс шара с центром основания шарового сегмента.

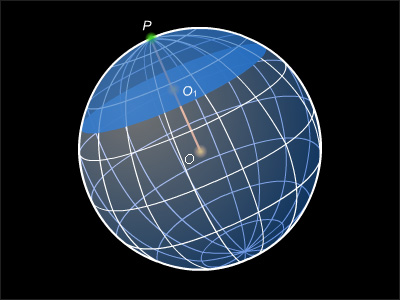
Шаровой сегмент можно рассматривать как тело, образованное вращением кругового сегмента вокруг диаметра, перпендикулярного его хорде. Формулу объема шарового сегмента выводят так же, как и формулу объема шара, но интегрируют на промежутке (0; H) (H – высота шарового сегмента): $V = π \int_{0}^{H} (2 R x - x^{2}) d x = π (R x^{2} - \frac{x^{3}}{3}) | \begin{array}{l} {}^{H} \\ {}_{0} \end{array} = π (R H^{2} - \frac{1}{3} H^{3}) .$

Следовательно, объем шарового сегмента равен $V = \frac{1}{3} π H^{2} (3 R - H) .$

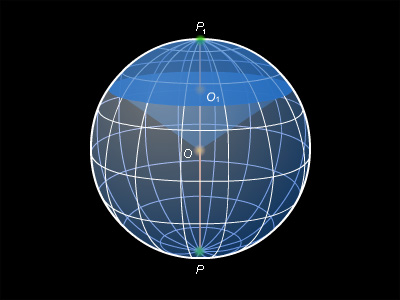
Шаровым сектором называется тело, образованное вращением кругового сектора вокруг оси, содержащей один из его граничных радиусов.

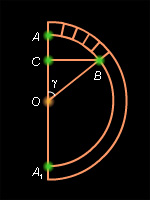
Шаровой сектор состоит из шарового сегмента и конуса. Поэтому его объем является суммой объемов шарового сегмента V₁ и конуса V₂: V = V₁ + V₂. Высота P₁O₁ шарового сегмента является также высотой и шарового сектора. Имеем $V_{1} = \frac{1}{3} π H^{2} (3 R - H),$ $V_{2} = \frac{1}{3} π r^{2} (R - H),$

где r – радиус конуса. Пусть P₁, P₂ – полюса шара, O₁A = r. Из прямоугольного треугольника P₁AP₂ находим r² = H (2R–H), следовательно, $V_{2} = \frac{1}{3} π H (2 R - H) (R - H) .$

Объем шарового сектора $V = \frac{1}{3} π H^{2} (3 R - H) + \frac{1}{3} π H (2 R - H) (R - H) = \frac{2}{3} π R^{2} H,$ или $V = \frac{2}{3} π R^{2} H .$

Смотрите также: Математика, Английский язык, Химия, Биология, Физика, География, Астрономия.
А также: библиотека ЭОРов и образовательный онлайн-сервис с тысячами интерактивных работ "Облако знаний".

Учебник. Объем частей шара

ГЛАВНАЯ

НОВОСТИ

УЧЕБНИК

ДОСТУП К БЕСПЛАТНЫМ УРОКАМ