Учебник. Вписанные и описанные многогранники

ГЛАВНАЯ

  

НОВОСТИ

  

УЧЕБНИК

  

ДОСТУП К БЕСПЛАТНЫМ УРОКАМ


Вписанные и описанные многогранники

Выпуклый многогранник называется вписанным, если все его вершины лежат на некоторой сфере. Эта сфера называется описанной для данного многогранника.

Выпуклый многогранник называется описанным, если все его грани касаются некоторой сферы. Эта сфера называется вписанной для данного многогранника.

При рассмотрении понятий вписанной и описанной сферы обнаруживается аналогия с понятием вписанной и описанной окружности. Однако, если в любой треугольник можно вписать окружность и около любого треугольника можно описать окружность, то не всякий многогранник является вписанным или описанным. Несмотря на это, оказывается, что пространственный аналог треугольника – треугольная пирамида, тем не менее, всегда имеет единственную вписанную и описанную сферу. Докажем это.

Треугольная пирамида имеет единственную описанную сферу.

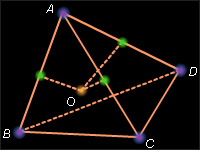
Поступим аналогично доказательству существования единственной окружности, описанной около данного треугольника. В данной пирамиде ABCD построим плоскости, перпендикулярные соответственно ребрам AB, AC и b>AD и проходящие через их середины. Эти плоскости будут равноудалены от точек A и B, A и C, A и D соответственно, поскольку геометрическим местом точек, равноудаленных от концов данного отрезка, является плоскость, проходящая через его середину и перпендикулярная ему. Обозначим точку пересечения этих плоскостей через O. Докажем, что эта точка существует и единственна. Действительно, две из этих плоскостей пересекаются по прямой l, поскольку они перпендикулярны двум непараллельным прямым. Эта прямая перпендикулярна к плоскости ABC. Плоскость, перпендикулярная AD, не параллельна l и не содержит её, поскольку в противном случае прямая AD перпендикулярна l, то есть лежит в плоскости ABC. Итак, точка O равноудалена от всех вершин треугольной пирамиды, значит эта точка является центром описанной сферы. Тем самым доказано существование такой сферы.

Докажем теперь её единственность. Заметим, что центр любой другой сферы, проходящей через все вершины пирамиды, равноудален от всех этих вершин и, значит, принадлежит всем плоскостям, проходящим через середины ребер перпендикулярно последним. А это и означает, что центр такой сферы и точка O совпадают.

Треугольная пирамида имеет единственную вписанную сферу.

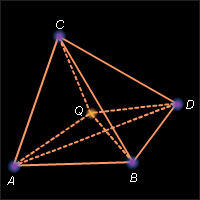
В треугольной пирамиде ABCD проведём биссекторные плоскости её двугранных углов с рёбрами AB, AC и DC. Эти плоскости имеют единственную общую точку Q, что доказывается аналогично предыдущей теореме. Понятно, что точка Q равноудалена от всех граней пирамиды. Таким образом, установлено существование вписанной сферы, единственность которой доказывается опять-таки аналогично.

Для того, чтобы пирамида была вписанной в сферу, необходимо и достаточно, чтобы её основанием был вписанный в окружность многоугольник.

Любая правильная пирамида является вписанной.

Пусть центр сферы, описанной вокруг пирамиды, лежит на прямой, проходящей через высоту пирамиды. Тогда

  1. b2 = 2RH,

  2. r2 = H(2R – H),

где R – радиус описанной сферы, H и b – соответственно высота и боковое ребро пирамиды, а r – радиус окружности, описанной вокруг основания пирамиды.

Пусть PO – высота пирамиды, O' – центр описанной сферы (чертеж 5.6.1). Поскольку O' ∈ PO, то O – центр окружности, описанной вокруг основания пирамиды. PK – диаметр описанной сферы, ΔAPK – прямоугольный. Согласно свойствам прямоугольного треугольника, имеем:

  1. AO2 = PO · KO, или r2 = H(2R – H);

  2. PA2 = PK · KO, или b2 = 2RH.

Если сфера вписана в многогранник, то объем этого многогранника равен V= 1 3 r S п , где S п  – площадь полной поверхности многогранника, r – радиус вписанной сферы.

Соединим центр вписанной сферы со всеми вершинами многогранника. При этом многогранник делится на несколько пирамид (их количество равно количеству граней многогранника). Высота каждой из этих пирамид равна r, а площадь основания – это площадь некоторой грани многогранника, поэтому V= 1 3 r S 1 + 1 3 r S 2 +...+ 1 3 r S m , (m – количество граней), V= 1 3 r( S 1 + S 2 +...+ S m ) = 1 3 r S п , что и требовалось доказать.

Поскольку центр вписанной сферы одинаково удален от всех граней многогранника, он лежит на пересечении биссекторных плоскостей всех двугранных углов многогранника.

В правильную n-угольную пирамиду можно вписать сферу.

На чертеже 5.6.2 изображена n-я часть правильной n-угольной пирамиды, где PC – апофема боковой грани PAB; CO' – биссектриса угла PCO. Ясно, что точка O' одинаково удалена от всех граней пирамиды и является центром вписанной сферы: OO' = r – радиус вписанной сферы.

Из ΔO'OC имеем: O'O = r = OC tg (α/2), или r = r1 tg (α/2), где r1 – радиус окружности, вписанной в основание пирамиды, α – двугранный угол при ребре основания.

 

 

Смотрите также: Математика, Английский язык, Химия, Биология, Физика, География, Астрономия.
А также: библиотека ЭОРов и образовательный онлайн-сервис с тысячами интерактивных работ "Облако знаний".

 

 

 

© Физикон, 1999-2015