
Учебник. Касания круглых тел с прямой и плоскостью
Касательной плоскостью к сфере называется плоскость, имеющая единственную общую точку со сферой.
Через любую точку A сферы проходит единственная касательная плоскость. Эта плоскость перпендикулярна радиусу OA сферы, где O – центр сферы.
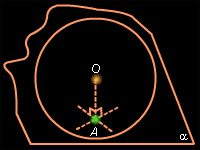
Пусть α – некоторая плоскость, проходящая через A и перпендикулярная OA (рис. 5.5.1). Все точки плоскости α, кроме точки A, удалены от точки O на расстояние большее, чем OA, поскольку кратчайший путь от точки до плоскости – это путь по перпендикуляру к плоскости. Значит, α – касательная плоскость. Обратно, если некоторая плоскость касается сферы в точке A, то A – ближайшая к O точка плоскости. Значит, эта плоскость совпадает с α.
Если расстояние от центра сферы до плоскости меньше радиуса сферы, то линия сечения сферы этой плоскостью – окружность.
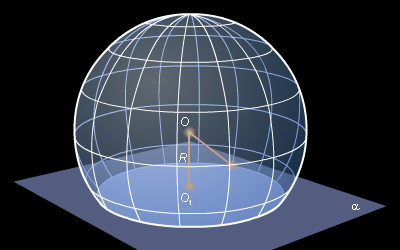
Пусть задана сфера ω (O, R) и плоскость α, O1 = ПpαO, OO1 < R по условию. Если произвольная точка A принадлежит линии пересечения сферы и плоскости, то OA = R. Из прямоугольного треугольника имеем Поскольку величины R и OO1 фиксированы, то и величина O1A фиксирована. Это означает, что точка пересечения плоскости α и сферы ω лежит на данном расстоянии от точки O1, следовательно, точка A лежит на окружности
Из теоремы следует, что, когда расстояние от центра шара до плоскости меньше радиуса, сечение шара этой плоскостью – круг. Если плоскость удалена от центра сферы на расстояние R, то она является касательной плоскостью.
Плоскости, равноудаленные от центра сферы, пересекают ее по равным окружностям.
Доказательство следует из того, что где r – радиус линии пересечения.
Ясно, что наибольшая окружность образуется при пересечении плоскостью, проходящей через центр сферы. Линия пересечения называется большой окружностью сферы. Соответствующее сечение шара называется большим кругом шара.
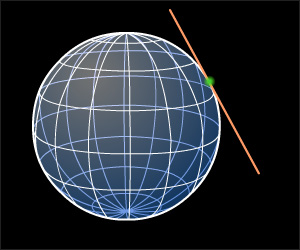
Прямая, проведенная через точку сферы перпендикулярно радиусу, проведенному в эту точку, называется касательной прямой к сфере.
Касательная прямая сферы имеет со сферой единственную общую точку.
Через любую точку сферы можно провести бесконечное число касательных прямых, причем все они лежат в касательной плоскости.
Плоскость, которая имеет с поверхностью конуса (цилиндра) единственную общую образующую, называется плоскостью, касающейся боковой поверхности конуса (цилиндра).
Определению 5.8 можно придать такой вид.
Прямая, касающаяся сферы – это прямая, которая имеет единственную общую точку со сферой.
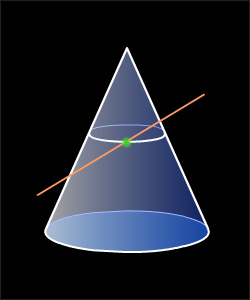
Аналогично можно ввести понятие касательной прямой к поверхности конуса (цилиндра), однако при этом рассматриваются прямые, не проходящие через точки на основании конуса (цилиндра) и через вершину конуса.
Так же несложно определяются понятия двух касающихся сфер и сферы, касающейся боковой поверхности конуса. Однако при решении задач, в которых фигурируют эти объекты, нужно быть предельно внимательным, поскольку существует два вида касания: внутреннее и внешнее.

А также: библиотека ЭОРов и образовательный онлайн-сервис с тысячами интерактивных работ "Облако знаний".