
Учебник. Правильный многоугольник
Выпуклый многоугольник называется правильным, если у него все стороны равны и все углы равны. Центром правильного многоугольника называется точка, равноудаленная от всех его вершин и всех его сторон. Центральным углом правильного многоугольника называется угол, под которым видна сторона из его центра.
Свойства правильного многоугольника.
Правильный многоугольник является вписанным в окружность и описанным около окружности, при этом центры этих окружностей совпадают.
Пусть A и B – две соседние вершины правильного многоугольника. Проведем биссектрисы углов многоугольника из вершин A и B. Пусть O – точка их пересечения. Треугольник AOB – равнобедренный с основанием AB и углами при основании, равными α / 2, где α – градусная мера угла многоугольника. Соединим точку O с вершиной C, соседней с B. Треугольники AOB и BOC равны по первому признаку равенства треугольников (теорема 4.1), так как AB = BC, OB – общая сторона, ∠OBC = α / 2 = ∠OBA. Отсюда имеем OC = OB = OA. ∠OCB = α / 2. Так как ∠C = α, то CO – биссектриса угла C. Аналогично, рассматривая последовательно вершины, соседние с ранее рассмотренными, получаем, что каждый треугольник, у которого одна сторона – сторона многоугольника, а противолежащая вершина – точка O, является равнобедренным. Все эти треугольники имеют равные боковые стороны и равные высоты, опущенные на основания. Отсюда следует, что все вершины треугольника равноудалены от точки O на расстояние длины боковой стороны и лежат на одной окружности, а все стороны многоугольника касаются окружности с центром в точке O и радиусом, равным высотам треугольников, опущенным из вершины O. Теорема доказана.
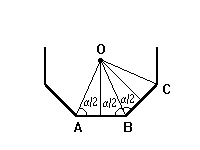
Центр правильного многоугольника совпадает с центрами вписанной и описанной окружностей.
Сторона правильного n-угольника связана с радиусом R описанной окружности формулой
Из Δ AOB что и требовалось доказать.
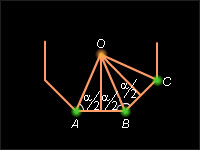
Периметры правильных n-угольников относятся как радиусы описанных окружностей.
А также: библиотека ЭОРов и образовательный онлайн-сервис с тысячами интерактивных работ "Облако знаний".