Учебник. Проведение перпендикуляра к данной прямой

Через точку O провести прямую, перпендикулярную данной прямой a.

Решение. Возможны два случая:

1. точка O лежит на прямой a;
2. точка O не лежит на прямой a.

Случай 1.

Анализ.
Пусть a – данная прямая, O – данная точка на ней, b – искомая прямая, перпендикулярная прямой a и проведенная через точку O. Из предыдущей задачи нам известен способ построения серединного перпендикуляра к отрезку AB. Тогда, если точка O – середина некоторого отрезка, то b – серединный перпендикуляр к этому отрезку и проходит через точку O.

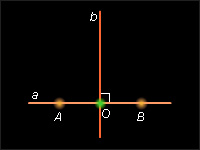
Построение.
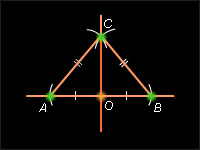
Отложим от точки O по разные стороны от нее на прямой a одинаковые отрезки OA, OB. Проведём две окружности одинакового радиуса AB с центром в точках A и B соответственно. Они пересекаются в точке C. Проведём прямую (OC). Она перпендикулярна прямой a.

Случай 2.

Анализ. Пусть O – данная точка, лежащая вне данной прямой a, b – прямая, проходящая через точку O и перпендикулярная прямой a. Чтобы построить прямую, нам необходимо указать (построить) ещё какую-либо её точку. Для этого проанализируем: какими свойствами обладают точки прямой b ⊥ a? В частности, любые две равные наклонные к прямой a, проведенные из точки O, имеют одинаковые проекции. Поэтому, если OA = OB – такие наклонные, то должно быть AC = CB, где C – точка пересечения прямых a и b.

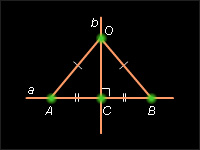
Построение.
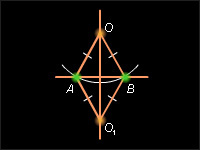
Проведём окружность с центром в точке O, пересекающую прямую a в двух точках A и B. Проведём две окружности с центрами в точках A и B и радиусом, равным OA. Пусть O₁ – точка пересечения, отличная от точки O, (O и O₁ лежат в разных полуплоскостях). Тогда прямая (OO₁) перпендикулярна данной прямой a.

Через точку O проведите прямую, перпендикулярную данной.