
Учебник. Деление отрезка пополам
Анализ. Пусть [AB] – данный отрезок, точка O – его середина, прямая a – серединный перпендикуляр к отрезку AB. Выберем произвольную точку C на прямой a, отличную от точки O. В треугольнике ACB CO – одновременно медиана и высота. Следовательно, треугольник ACB равнобедренный, и AC = BC. Отсюда возникает следующий способ построения точки O – середины отрезка AB.
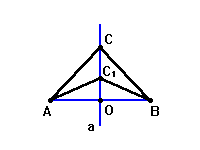
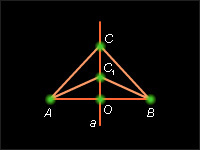
Построение. Из точек A и B циркулем описывается окружность радиусом AB. Пусть C и C1 – точки пересечения этих окружностей. Они лежат в разных полуплоскостях относительно прямой AB. С помощью линейки соединить точки C и C1. Отрезок CC1 пересекает отрезок AB в точке O. Эта точка – середина отрезка AB.
Нужно поделить отрезок AB пополам и середину отрезка обозначить точкой O.
Соединим точки C и C1 с концами отрезка AB. По построению AC1 = AC = C1B = CB. Поэтому равнобедренные треугольники CAC1 и CBC1 равны по трем сторонам. Отсюда следует равенство углов ACO и BCO. В равнобедренном треугольнике ABC CO – биссектриса, проведенная к основанию, следовательно, она медиана и высота. Отсюда AO = OB, и точка O – середина отрезка AB.
А также: библиотека ЭОРов и образовательный онлайн-сервис с тысячами интерактивных работ "Облако знаний".