
Учебник. Параллелограмм
Параллелограммом называется четырёхугольник, у которого противолежащие стороны попарно параллельны.
Высотой параллелограмма, проведенной к данной его стороне, называется перпендикуляр, опущенный из произвольной точки противолежащей стороны к прямой, содержащей
Признаки параллелограмма.
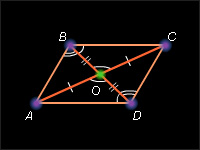
Если диагонали четырёхугольника пересекаются и точкой пересечения делятся пополам, то такой четырёхугольник – параллелограмм.
Пусть ABCD – данный четырёхугольник. По условию AO = OC, BO = OD. Так как
Если у четырёхугольника пара противоположных сторон параллельны и равны, то четырёхугольник – параллелограмм.
Пусть ABCD – данный четырёхугольник и (AB) || (CD), AB = CD.
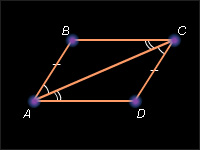
Проведём диагональ AC. Получившиеся треугольники ABC и ADC равны. Действительно, стороны AB и CD равны по условию, сторона AC – общая,
Если у четырёхугольника противолежащие стороны попарно равны, такой четырёхугольник – параллелограмм.
Пусть ABCD – данный четырёхугольник, и AB = CD, BC = AD.
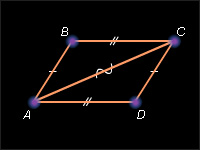
Проведём диагональ AC. Получившиеся треугольники ABC и CDA равны по трем сторонам. Действительно,
Если в четырёхугольнике противолежащие углы равны, такой четырёхугольник – параллелограмм.
Пусть ABCD – данный четырёхугольник, и ∠ B = ∠ D, ∠ A = ∠ C. Проведём диагональ AC.
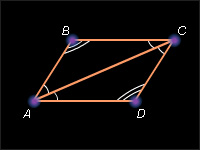
Сумма углов четырёхугольника равна сумме углов треугольника ABC и треугольника ACD. Так как сумма углов каждого треугольника – 180°, то ∠A + ∠B + ∠C + ∠D = 360°. С учетом условия получаем, что
Углы A и D являются внутренними односторонними при
Свойствa параллелограмма.
Диагонали параллелограмма пересекаются и точкой пресечения делятся пополам.
Пусть ABCD – данный параллелограмм. По определению (AB) || (CD) и (AD) || (BC). Пусть O – середина диагонали BD и на луче, дополняющем луч OA, отложен отрезок OC1, равный отрезку OA. По теореме 7.1 получившийся четырёхугольник ABC1D – параллелограмм, и, следовательно, (BC1) || (AD) и (AB) || (C1D). С учетом условия – (BC) || (AD) и (AB) || (CD). В соответствии с теоремой 3.3 (BC) = (BC1) и (DC) = (DC1). Поэтому точки C и C1 совпадают. Следовательно, совпадают параллелограммы ABCD и ABC1D. Отсюда AO = OC и BO = OD. Теорема доказана.
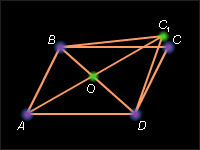
Параллелограмм – выпуклый четырёхугольник.
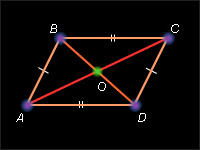
У параллелограмма противолежащие стороны равны, противолежащие углы равны.
Пусть ABCD – данный параллелограмм, т.е. (AB) || (CD) и (BC) || (AD) и O – точка пересечения диагоналей. Тогда AO = OC и BO = OD. Поскольку
В силу доказанного в треугольниках BAD и DCB AB = DC, AD = BC и BD – общая сторона и по теореме 4.8 Δ BAD = Δ DCB. Тогда ∠BCD = ∠BAD. Аналогично из равенства треугольников ABC и CDA следует равенство углов (ABC) и (CDA). Теорема доказана.
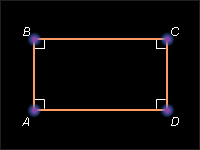
Прямоугольником называется параллелограмм, у которого все углы прямые.
Свойство прямоугольника задается следующей теоремой:
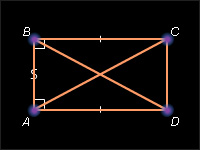
Диагонали прямоугольника равны.
Пусть ABCD – данный прямоугольник. Прямоугольные треугольники BAD и ABC равны
А также: библиотека ЭОРов и образовательный онлайн-сервис с тысячами интерактивных работ "Облако знаний".