Учебник. Прямоугольный треугольник

Аксиомы 1.4 и 2.1 позволяли приписывать отрезкам и углам числа, равные их мерам, то есть измерять отрезки и углы. До сих пор не было связи между величинами углов и длинами отрезков. С введением треугольников появляется возможность связать величины градусных мер углов треугольника и длин его сторон. Рассмотрим соотношения между сторонами и углами прямоугольного треугольника.

Прямоугольный треугольник

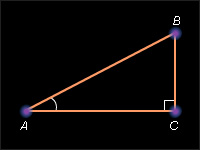
Косинусом острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе. Пусть угол (BAC) – искомый острый угол. Так, например, для угла BAC (рис. 5.1.1).

Пусть ABC и A₁B₁C₁ – два прямоугольных треугольника с одним и тем же углом при вершинах A и A₁, равным α . Построим треугольник AB₂C₂, равный треугольнику A₁B₁C₁, как показано на рис. 5.1.2. Это возможно по аксиоме 4.1. Так как углы A и A₁ равны, то B₂ лежит на прямой AB. Прямые BC и B₂C₂ перпендикулярны прямой AC, и по следствию 3.1 они параллельны. По теореме 4.13

$\frac{A{C}_2}{A{B}_2}=\frac{AC}{AB}.$

К теореме 5.1

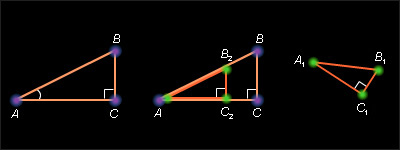
Но по построению AC₂ = A₁C₁; AB₂ = A₁B₁, следовательно,

$\frac{A_1{C}_1}{A_1{B}_1}=\frac{AC}{AB}\mathrm{.}$

Что и требовалось доказать.

На рисунке 5.1.3 изображен прямоугольный треугольник. BC и AC – его катеты, AB – гипотенуза. По теореме BC² + AC² = AB².

Пусть ABC – данный прямоугольный треугольник с прямым углом при вершине C.

К доказательству теоремы Пифагора

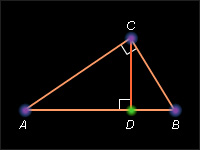
Проведем высоту CD из вершины C. По определению $cosA=\frac{AD}{AC}$ из треугольника ACD и $cosA=\frac{AC}{AB}$ из треугольника ABC. По теореме 5.1 $\frac{AD}{AC}=\frac{AC}{AB}$ и, следовательно, $ABċAD=A{C}^2$ . Аналогично $cosB=\frac{BD}{BC}$ из Δ CDB, $cosB=\frac{BC}{AB}$ из Δ ACB, и $\frac{BD}{BC}=\frac{BC}{AB}\mathrm{.}$ Отсюда AB ċ BD = BC². Складывая полученные равенства и, замечая, что AD + BD = AB, получаем AC² + BC² = AB ċ AD + AB ċ BD = AB (AD + BD) = AB². Теорема доказана.

В прямоугольном треугольнике любой из катетов меньше гипотенузы. Косинус любого острого угла меньше единицы.

Пусть [BC] – перпендикуляр, опущенный из точки B на прямую a, и A – любая точка этой прямой, отличная от C. Отрезок AB называется наклонной, проведенной из точки B к прямой a. Точка C называется основанием наклонной. Отрезок AC называется проекцией наклонной.

С помощью теоремы Пифагора можно показать, что если к прямой из одной точки проведены перпендикуляр и наклонные, то

• любая наклонная больше перпендикуляра,

• равные наклонные имеют равные проекции,

• из двух наклонных больше та, у которой проекция больше.

Синусом острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе. По определению $sin\mathrm{(}\mathrm{\angle }BAC\mathrm{)}=\frac{BC}{AB}\mathrm{.}$

Тангенсом острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему. Для угла (BAC) прямоугольного треугольника, изображенного на рис. 5.1.1, имеем $tg\mathrm{(}\mathrm{\angle }BAC\mathrm{)}=\frac{BC}{AC}\mathrm{.}$

Так же как и косинус, синус угла и тангенс угла зависят только от величины угла.

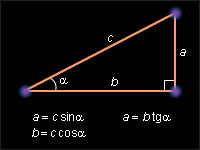
Из данных определений получаем следующие соотношения между углами и сторонами прямоугольного треугольника: если α – острый угол прямоугольного треугольника , то

• катет, противолежащий углу α , равен произведению гипотенузы на sin α;

• катет, прилежащий к углу α , равен произведению гипотенузы на cos α;

• катет, противолежащий углу α , равен произведению второго катета на tg α.