Учебник. Сумма углов треугольника

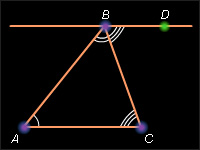
Пусть дан Δ ABC. Проведем через вершину B прямую, параллельную (AC) и отметим на ней точку D так, чтобы точки A и D лежали по разные стороны от прямой BC. Тогда ∠DBC и ∠ACB равны как внутренние накрест лежащие при параллельных прямых BD и AC и секущей (BC). Тогда сумма углов треугольника при вершинах B и C равна углу (ABD). Но угол (ABD) и угол (BAC) при вершине A треугольника ABC являются внутренними односторонними при параллельных прямых BD и AC и секущей (AB), и их сумма равна 180°. Следовательно, сумма углов треугольника равна 180°. Теорема доказана.

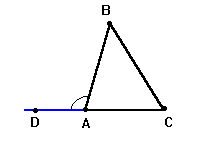
Пусть дан Δ ABC. Точка D лежит на прямой AC так, что A лежит между C и D. Тогда ∠BAD – внешний к углу треугольника при вершине A и ∠A + ∠BAD = 180°. Но ∠A + ∠B + ∠C = 180°, и, следовательно, ∠B + ∠C = 180° – ∠A. Отсюда ∠BAD = ∠B + ∠C. Следствие 4.2 доказано.

Внешний угол треугольника