Открытая Математика. Планиметия. Утверждения в математике

Утверждения в математике

В математике мы имеем дело с различными утверждениями, например,

A ≡ {число 100 делится на 4};
B ≡ {через две точки можно провести две прямые};
C ≡ {число 0,00000001 очень мало}.

Относительно одних утверждений можно сказать, что в них говорится нечто правильное, относительно других – утверждается нечто неверное. Например, утверждение A – верное, утверждение B – неверное. Относительно утверждения C нельзя сказать, является оно верным или нет, так как оно не имеет точного смысла.

Утверждение, которое является верным, называется истинным.

Утверждение, которое является неверным, называется ложным.

Высказыванием называется любое утверждение, о котором можно сказать, истинно оно или ложно.

Из определения 16.14 вытекает

Всякое высказывание является либо истинным, либо ложным (закон исключенного третьего).

Никакое высказывание не может быть одновременно истинным и ложным (закон противоречия).

Предложение, о котором невозможно однозначно решить вопрос, истинно оно или ложно, высказыванием не является.

На множестве высказываний можно ввести операции, позволяющие образовывать новые высказывания. Например, если заданы два высказывания A{сейчас солнечно} и B{сейчас ветрено}, то с помощью связок «и», «или», «если..., то...», «либо..., либо...», «тогда и только тогда, когда», «неверно, что» можно образовать новые высказывания вида: {сейчас солнечно и ветрено}, {сейчас солнечно или ветрено}, {если сейчас солнечно, то сейчас ветрено} и т.д. Такие высказывания называют составными, а входящие в них высказывания A и B – элементарными.

Два составных высказывания A и B называются равносильными, если они одновременно истинны или одновременно ложны при любых предположениях относительно истинности входящих в них элементарных высказываний. В этом случае пишут A = B.

Отрицанием высказывания A называется высказывание, которое истинно, когда A ложно, и ложно, если A истинно. Обозначение: $\bar{A} .$ Читается: «неверно, что A».

Данное определение записывают с помощью таблицы истинности, в которой буква «И» означает истинное высказывание, а буква «Л» – ложное.

A	И	Л
$\bar{A}$	$Л$	$И$

Например: отрицанием высказывания {через две точки можно провести две прямые} является высказывание {через две точки нельзя провести две прямые}. Отрицанием высказывания {число 37 не делится на 2} будет высказывание {число 37 делится на 2}.

Конъюнкцией двух высказываний A и B называется высказывание, которое истинно в том и только в том случае, если истинны оба высказывания. Обозначение: $A \land B$ , читается: «A и B». Таблица истинности имеет вид:

A	И	И	Л	Л
B	И	Л	И	Л
$A \land B$	$И$	$Л$	$Л$	$Л$

Например: конъюнкцией высказываний {3 < 8} и {8 < 11} является высказывание {3 < 8 < 11}. Или, конъюнкцией высказываний {точка A лежит на прямой a} и {точка A лежит на прямой b} является высказывание {точка A лежит на прямой a и на прямой b}.

Дизъюнкцией двух высказываний A и B называется высказывание, которое ложно тогда и только тогда, когда ложны оба высказывания. Обозначение: $A \lor B$ , читается: «A или B». Таблица истинности имеет вид:

A	И	И	Л	Л
B	И	Л	И	Л
$A \lor B$	$И$	$И$	$И$	$Л$

Примеры: дизъюнкцией высказываний

{3 < 8} и {3 = 8} является высказывание {3 < 8 < 11};
{точка A лежит на прямой a} и {точка A лежит на прямой b} является высказывание {точка A лежит на прямой a или на прямой b}, где связка "или" не имеет разделительного смысла. То есть точка A может лежать либо только на прямой a, либо только на прямой b, либо же на прямой a и прямой b одновременно.

Операции дизъюнкции и конъюнкции коммутативны. $A \lor B = B \lor A$ и $A \land B = B \land A$ .

Для доказательства достаточно сравнить таблицы истинности высказываний $A \lor B$ и $B \lor A$ ( $A \land B$ и $B \land A).$ Покажем для $A \lor B$ и $B \lor A$ .

A	И	И	Л	Л
B	И	Л	И	Л
$A \lor B$	$И$	$И$	$И$	$Л$

B	И	И	Л	Л
A	И	Л	И	Л
$B \lor A$	$И$	$И$	$И$	$Л$

Операции дизъюнкции и конъюнкции ассоциативны. $A \lor (B \lor C) = (A \lor B) \lor C$ и $A \land (B \land C) = (A \land B) \land C .$

Высказывание $A \land (B \land C)$ истинно только если одновременно истинны A, B и C, а во всех других случаях – ложно. Высказывание $(A \land B) \land C$ также истинно, только если A, B и C одновременно истинны. Совпадение истинности двух высказываний доказывает их эквивалентность. Аналогично высказывание $A \lor (B \lor C)$ ложно, только если ложны одновременно все три высказывания A, B и C, но в этом случае ложно и $(A \lor B) \lor C .$ Во всех остальных случаях оба высказывания $A \lor (B \lor C)$ и $(A \lor B) \lor C$ – истинны. Следовательно, $A \lor (B \lor C) = (A \lor B) \lor C .$

Для любых трех высказываний A, B и C справедливы равенства $(A \lor B) \land C = (A \land C) \lor (B \land C);$
$(A \land B) \lor C = (A \lor C) \land (B \lor C) .$

Пусть $(A \lor B) \land C$ – истинно. Это возможно, только если истинны C и $(A \lor B),$ а это значит, что C – истинно, а A и B не являютя одновременно ложными. Отсюда следует, что истинным является одно из двух высказываний $(A \land C)$ или $(B \land C),$ то есть $(A \land C) \lor (B \land C)$ – истинно. Далее, если $(A \lor B) \land C$ – ложно, то C и $(A \lor B)$ не являются одновременно истинными, то есть либо C ложно, либо ложно $(A \lor B),$ или либо ложно C, либо ложны одновременно A и B. Отсюда одновременно ложны $(A \land C)$ и $(B \land C),$ то есть ложно $(A \land C) \lor (B \land C) .$ Следовательно, высказывания по определению равносильны и справедливо равенство $(A \lor B) \land C = (A \land C) \lor (B \land C) .$

Пусть $(A \land B) \lor C$ – истинно. Тогда истинно либо C, либо $(A \land B),$ то есть либо истинно C, либо одновременно истинны A и B. В любом случае тогда истинны $(A \lor C)$ и $(B \lor C)$ одновременно, а значит, истинно $(A \lor C) \land (B \lor C) .$ Если же $(A \land B) \lor C$ – ложно, то одновременно ложны и C, и $(A \land B),$ то есть C – ложно, а A и Bне являются одновременно истинными (либо A ложно, либо B ложно). Тогда ложно либо $(A \lor C),$ либо $(B \lor C),$ то есть $(A \lor C) \land (B \lor C)$ – ложно. Отсюда $(A \land B) \lor C = (A \lor C) \land (B \lor C) .$

Дизъюнкция любого высказывания A и его отрицания $\bar{A}$ – тождественно истинна. Обозначение: $A \lor \bar{A} = И .$

Для любых двух высказываний A и B справедливы формулы де Моргана: $a) \bar{A \land B} = \bar{A} \lor \bar{B};$ $б) \bar{A \lor B} = \bar{A} \land \bar{B} .$

а) Составим таблицы истинности правой и левой частей равенства.

A И И Л Л

B И Л И Л

$A \land B$ $И$ $Л$ $Л$ $Л$

$\bar{A \land B}$ $Л$ $И$ $И$ $И$

A И И Л Л

B И Л И Л

$\bar{A}$ $Л$ $Л$ $И$ $И$

$\bar{B}$ $Л$ $И$ $Л$ $И$

$\bar{A} \lor \bar{B}$ $Л$ $И$ $И$ $И$

Сравнивая последние строчки таблицы, приходим к требуемому равенству.
б) Аналогично, сравнивая таблицы истинности правой и левой частей, получаем их равносильность:

A И И Л Л

B И Л И Л

$A \lor B$ $И$ $И$ $И$ $Л$

$\bar{A \lor B}$ $Л$ $Л$ $Л$ $И$

A И И Л Л

B И Л И Л

$\bar{A}$ $Л$ $Л$ $И$ $И$

$\bar{B}$ $Л$ $И$ $Л$ $И$

$\bar{A} \land \bar{B}$ $Л$ $Л$ $Л$ $И$

Высказывание «если A, то B» называют импликацией высказываний A и B, если оно ложно лишь в случае, когда A – истинно, а B – ложно. Обозначение: $A \Rightarrow B .$ Таблица истинности имеет вид:

A	И	И	Л	Л
B	И	Л	И	Л
$A \Rightarrow B$	$И$	$Л$	$И$	$И$

Высказывание A называют условием, а B – заключением импликации.

Для любых двух высказываний A и B справедливо $(A \Rightarrow B) = (\bar{A} \lor B) .$

Следует из сравнения таблиц истинности:

A И И Л Л

B И Л И Л

$\overset{&¯}{A}$ $Л$ $Л$ $И$ $И$

$A \Rightarrow B$ $И$ $Л$ $И$ $И$

$\bar{A} \lor B$ $И$ $Л$ $И$ $И$

$A$ $B$ $\overset{&¯}{A}$ $\overset{&¯}{B}$ $A \Rightarrow B$ $\bar{B} \Rightarrow \bar{A}$ $B \Rightarrow A$ $\bar{A} \Rightarrow \bar{B}$

И И Л Л И И И И

И Л Л И Л Л И И

Л И И Л И И Л Л

Л Л И И И И И И

Импликацией, обратной данной импликации $A \Rightarrow B$ , называется импликация $B \Rightarrow A$ .

Импликацией, противоположной данной импликации $A \Rightarrow B$ , называется импликация $\bar{A} \Rightarrow \bar{B}$ .

Например: импликацией высказываний {100 делится на 4} и {100 – четное число} является высказывание {если 100 делится на 4, то 100 – четное число}. Импликация обратная данной будет тогда такой: {если 100 – четное число, то 100 делится на 4}. Как мы видим, если импликация истинна, то обратная к ней не всегда будет истинна. Противоположной к исходной будет импликация {если 100 не делится на 4, то 100 не является четным числом}.

Справедливы равенства $(A \Rightarrow B) = (\bar{B} \Rightarrow \bar{A})$ и $(B \Rightarrow A) = (\bar{A} \Rightarrow \bar{B}) .$

См. доказательство свойства 16.14.

Эквиваленцией высказываний A и B называется высказывание, которое истинно, когда оба высказывания A и B истинны или оба ложны. Обозначение: $A \Leftrightarrow B .$ Таблица истинности имеет вид:

A	И	И	Л	Л
B	И	Л	И	Л
$A \Leftrightarrow B$	$И$	$Л$	$Л$	$И$

Например: эквиваленцией двух высказываний {точки A и B лежат в разных полуплоскостях от прямой a} и {отрезок AB пересекает прямую a} является высказывание {точки A и B лежат в разных полуплоскостях от прямой a тогда и только тогда, когда отрезок AB пересекает прямую a}.

Пусть предложение содержит переменную, которая может принимать различные значения, причем подстановка любого из значений переменной превращает предложение в высказывание. Тогда это предложение называют одноместным предикатом. Множество X всех значений переменной x называют областью определения предиката. Обозначение предиката: A (x).

Множеством истинности предиката A (x), x∈X называется подмножество T⊂X, на котором A (x) истинно.

Например: на рис. 16.3.2 изображены точки, соединенные несколькими отрезками. На множестве X, состоящем из точек a, b, c, d, e, f, g (X = {a, b, c, d, e, f, g}), задан одноместный предикат A (x) = {к точке x в рассматриваемой фигуре примыкают три отрезка}.

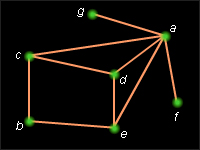
Ниже приведена таблица истинности этого предиката:

A (a)	A (b)	A (c)	A (d)	A (e)	A (f)	A (g)
Л	Л	И	И	И	Л	Л

Множеством истинности данного предиката, соответственно, будет множество точек T = {c, d, e}.

Два предиката A (x) и B (x) называются эквивалентными, если у них совпадают области определения и множества истинности. Обозначение: $A (x) \sim B (x) .$

Квантором общности называют символ $∀$ , означающий слово «все». Высказывание $(∀ x \in X) P (x)$ читается: «для всех x из X справедливо P от x».
Квантором существования называют символ $∃$ , означающий слово «существует». Высказывание $(∃ x \in X) P (x)$ читается: «существует такое x из X, что справедливо P от x».

Справедливо а) $\bar{(∀ x) A (x)} = (∃ x) \bar{A (x)};$ б) $\bar{(∃ x) A (x)} = (∀ x) \bar{A (x)} .$

а) Если истинно высказывание $(∀ x) A (x),$ то это означает, что не для всех x выполнено A (x), другими словами, существует x, для которого выполнено $\bar{A (x)},$ то есть когда истинно выражение $(∃ x) \bar{A (x)} .$ Если $\bar{(∀ x) A (x)}$ – ложно, то $(∀ x) A (x)$ – истинно, тогда $(∃ x) \bar{A (x)}$ – ложно. Это доказывает равносильность высказываний и равенство $\bar{(∀ x) A (x)} = (∃ x) \bar{A (x)} .$
б) Так как формула пункта а) верна для любого предиката A (x), возьмем предикат $\bar{A (x)} .$ Получим $\bar{(∀ x) \bar{A (x)}} = (∃ x) \bar{\bar{A (x)}} = (∃ x) A (x) .$ Строя отрицание обеих частей, получаем $\bar{\bar{(∀ x) \bar{A (x)}}} = \bar{(∃ x) A (x)} .$ С учетом того, что для любого высказывания $\bar{\bar{A}} = A,$ имеем $(∀ x) \bar{A (x)} = \bar{(∃ x) A (x)},$ что и требовалось доказать.

Так же, как и для высказываний, на множестве предикатов можно ввести операции отрицания, конъюнкции, дизъюнкции, импликации и эквиваленции. Для этого устанавливают правила, которые позволяют находить множество истинности составного предиката, если известны множества истинности составляющих его элементарных предикатов.

Пусть на множестве X заданы предикаты A (x) и B (x), множества истинности которых соответственно $T_{1} \subset X$ и $T_{2} \subset X .$

Отрицанием предиката A (x) называется предикат $\bar{A (x)}, x \in X,$ множество истинности T которого является дополнением к множеству T₁, то есть T = X \ T₁.

Конъюнкцией предикатов A (x) и B (x) называется предикат $A (x) \land B (x), x \in X,$ множество истинности которого определяется равенством $T = T_{1} \cap T_{2} .$

Дизъюнкцией предикатов A (x) и B (x) называется предикат $A (x) \lor B (x), x \in X,$ множество истинности которого определяется равенством $T = T_{1} \cup T_{2} .$

Импликацией предикатов A (x) и B (x) называется предикат $A (x) \Rightarrow B (x), x \in X,$ множество истинности которого определяется равенством $T = T_{1}^{'} \cup T_{2},$ где $T' = X \\ T_{1} .$

В том случае, когда импликация $A (x) \Rightarrow B (x), x \in X$ истинна при всех значениях из множества X, говорят, что предикат B (x) логически следует из предиката A (x), и предикат B (x) называют необходимым условием для предиката A (x), а предикат A (x) – достаточным условием для B (x).

Если предикаты A (x) и B (x) на множестве X эквивалентны, то каждый из них называют необходимым и достаточным условием для второго.

Например, в импликации {если x – число натуральное, то оно целое} предикат B (x) = {x – число целое} логически следует из предиката A (x) = {x – число натуральное}. Следовательно, предикат B (x) является необходимым условием для предиката A (x), а предикат A (x) – достаточным для B (x). Используя эти термины, импликацию {если число x натуральное, то оно целое} можно выразить так:

Для того чтобы число x было натуральным, необходимо, чтобы оно было целым.
Для того чтобы число x было целым, достаточно, чтобы оно было натуральным.

Часто приходится рассматривать предикаты, в которые входит не одна, а две и больше переменных. Они называются в зависимости от числа переменных двухместными, трехместными, ..., n-местными. Рассмотрим, например, следующие предложения, в которых под x и y понимают произвольные натуральные числа: A (x, y) = {x < y}, B (x, y) = {x + y = 10}, C (x, y) = {x делится на y}, D (x, y) = {x + y есть простое число}.

Мы ничего не можем сказать об истинности или ложности этих утверждений, пока не сказано, какие значения принимают x и y. Но если точно указано, чему равны x и y, каждое из сформулированных утверждений превращается в высказывание – для одних пар (x, y) истинное, для других ложное. Множество всех пар чисел (x, y), для которых данный двухместный предикат есть истинное высказывание, называется множеством его истинности.

Приведем примеры высказываний, получающихся из указанных предложений при конкретных значениях x и y:

A (1; 3) = {1 < 3} – истинное высказывание,
A (2; 2) = {2 < 2} – ложное высказывание,
A (5; 4) = {5 < 4} – ложное высказывание,
B (1; 3) = {1 + 3 = 10} – ложное высказывание,
B (8; 2) = {8 + 2 = 10} – истинное высказывание и т.д.

Смотрите также: Математика, Английский язык, Химия, Биология, Физика, География, Астрономия.
А также: библиотека ЭОРов и образовательный онлайн-сервис с тысячами интерактивных работ "Облако знаний".

Учебник. Утверждения в математике

ГЛАВНАЯ

НОВОСТИ

УЧЕБНИК

ДОСТУП К БЕСПЛАТНЫМ УРОКАМ

A	И	И	Л	Л
B	И	Л	И	Л
$\overset{&¯}{A}$	$Л$	$Л$	$И$	$И$
$A \Rightarrow B$	$И$	$Л$	$И$	$И$
$\bar{A} \lor B$	$И$	$Л$	$И$	$И$

$A$	$B$	$\overset{&¯}{A}$	$\overset{&¯}{B}$	$A \Rightarrow B$	$\bar{B} \Rightarrow \bar{A}$	$B \Rightarrow A$	$\bar{A} \Rightarrow \bar{B}$
И	И	Л	Л	И	И	И	И
И	Л	Л	И	Л	Л	И	И
Л	И	И	Л	И	И	Л	Л
Л	Л	И	И	И	И	И	И