
Учебник. Отношения между множествами
Пусть во множестве A задано некоторое отношение "ˆ".
Отношение "ˆ" рефлексивно, если для любого элемента a из множества A выполнено aˆa (т.е. любой элемент связан отношением ˆ с самим собой).
Например: отношение равенства на множестве отрезков рефлексивно, так как любой отрезок равен сам себе.
Отношение ˆ симметрично, если из aˆb следует bˆa для любых элементов a и b множества A. Отношение равенства на множестве отрезков является симметричным, так как если [AB] = [CD], то и [CD] = [AB].
Отношение ˆ называется транзитивным, если из того, что aˆb и bˆc следует, что aˆc. В частности, отношение равенства отрезков рефлексивно, так как если отрезок AB равен отрезку CD, а отрезок CD равен отрезку MN, то отрезок AB равен отрезку MN.
Отношение ˆ во множестве A называется отношением эквивалентности, если оно одновременно рефлексивно, симметрично и транзитивно.
Всякое отношение эквивалентности во множестве A позволяет специальным образом различать элементы этого множества. Обозначим через C (a) множество всех элементов x из A, таких, что Это множество является подмножеством A, которое называется классом эквивалентности a. Если то в силу симметричности и транзитивности отношения любой элемент x, эквивалентный a, эквивалентен и b. Если же b не эквивалентен a, то C (a) и C (b) не имеют общих элементов, потому что если и , то в силу симметричности и , и в силу транзитивности что противоречит условию. Таким образом, отношением эквивалентности множество A разбивается на непересекающиеся классы эквивалентности, при котором каждый элемент A попадает в свой класс.
Как мы видели в приведенных выше примерах, равенство на множестве отрезков является отношением эквивалентности и задает его разбиение на классы эквивалентности. Каждый такой класс содержит отрезки заданной длины.
Пересечением множеств A и B называется множество, в которое входят те и только те элементы, которые одновременно принадлежат множествам A и B (общие элементы множеств A и B). Обозначение: A∩B, где символ ∩ – знак пересечения двух множеств. Два множества пересекаются, если A∩B ≠ ∅, и не пересекаются, если A∩B = ∅.
Например: если две прямые a и b не пересекаются, то можно записать a∩b = ∅, если же они пересекаются, то по определению их пересечением является общая точка A (a∩b = A). Пересечением луча a с дополняющим его лучом a' является их общее начало O (a∩a' = O).
Объединением двух множеств A и B называется множество, состоящее из тех элементов, которые принадлежат хотя бы одному из этих множеств. Обозначение: A∪B, где символ ∪ – знак объединения множеств.
Например: объединением луча a с дополняющим его лучом a' является прямая.
Разностью двух множеств A и B называется такое множество, в которое входят все те элементы, которые принадлежат A и не принадлежат B. Обозначение: A \ B. Если B – подмножество A, то A \ B называют дополнением к B и обозначают B'.
Например: разностью прямой a и ее луча с началом O является множество точек дополняющего луча a' без начальной точки O.
Введенные операции обладают рядом свойств.
Пересечение и объединение множеств коммутативно (перестановочно): A∩B = B∩A; A∪B = B∪A.
Эти свойства вытекают из определения. Действительно, пусть x∈A∩B, тогда x∈A и x∈B, следовательно, x∈B∩A. Отсюда (A∩B)⊂(B∩A). Аналогично доказывается обратное утверждение (B∩A)⊂(A∩B). Отсюда A∩B = B∩A.
Пусть x∈A∪B, тогда либо x∈A, либо x∈B, но тогда x∈B∪A и (A∪B)⊂(B∪A). Аналогично (B∪A)⊂(A∪B). Следовательно, A∪B = B∪A.
Пересечение и объединение множеств ассоциативно: для любых множеств A, B и C имеем
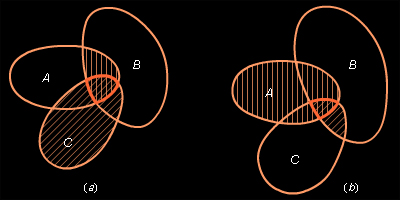
Пусть x∈(A∩B)∩C, отсюда x∈(A∩B) и x∈C, или x∈A, x∈B, x∈C. Отсюда x∈(B∩C) и x∈A, следовательно, x∈A∩(B∩C) и верно (A∩B)∩C⊂A∩(B∩C). Наоборот, если x∈A∩(B∩C), следует, что x∈A, x∈C, x∈B, откуда x∈(A∩B)∩C и верно A∩(B∩C)⊂(A∩B)∩C. Отсюда A∩(B∩C) = (A∩B)∩C (см. рис. 16.2.1 a), b)). Аналогично доказывается равенство множеств A∪(B∪C) = (A∪B)∪C.
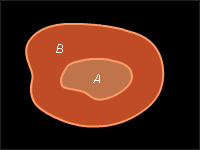
Если A⊂B, то A∩B = A, A∪B = B.
Пусть x∈A∩B, то есть x∈A и x∈B, отсюда x∈A. Пусть теперь x∈A. Из условия A⊂B следует, что x∈B, отсюда x∈A∩B. Следовательно, A∩B = A.
Пусть x∈A∪B, тогда x∈A или x∈B. Но A⊂B, и, следовательно, x∈B, A∪B⊂B. Если x∈B, то по определению x∈A∪B и верно включение B⊂A∪B. Отсюда A∪B = B (см. рис. 16.2.2).

Связь операций пересечения и объединения множеств отражает свойство дистрибутивности.
Для любых множеств A, B и C справедливы равенства:
а) A∩(B∪C) = (A∩B)∪(A∩C),
б) A∪(B∩C) = (A∪B)∩(A∪C).
а) Пусть x∈A∩(B∪C). Тогда x∈A и x∈(B∪C)→x∈A, x∈B или x∈C→x∈A∩B или x∈A∩C→x∈(A∩B)∪(A∩C)A∩(B∪C)⊂(A∩B)∪(A∩C). Пусть x∈(A∩B)∪(A∩C). Тогда x∈(A∩B) или x∈(A∩С)→(x∈A, x∈B) или (x∈A, x∈C)→x∈A и x∈B или x∈C→x∈A∩(B∪C) и отсюда (A∩B)∪(A∩C)⊂A∩(B∪C). Окончательно имеем A∩(B∪C) = (A∩B)∪(A∩C) (см. рис. 16.2.3 a), b)).

Понятия множества и подмножества используются при определении многих понятий математики и, в частности, при определении геометрической фигуры.
Определим как универсальное множество плоскость. Тогда можно дать следующее определение геометрической фигуры в планиметрии.
Геометрической фигурой называется всякое множество точек плоскости.
Таким образом, как сама точка, так и конечное и бесконечное множество точек являются геометрическими фигурами.
Из определения 16.11 непосредственно следует, что объединение и пересечение геометрических фигур есть геометрическая фигура.
Если фигура F1 явлется собственным подмножеством фигуры F2, то говорят также, что F1 – часть фигуры F2. Например, отрезок AB – часть прямой.
Чтобы наглядно отображать множества и отношения между ними, рисуют геометрические фигуры, которые находятся между собой в этих отношениях. Такие изображения множеств называют диаграммами Эйлера–Венна. Диаграммы Эйлера–Венна делают наглядными различные утверждения, касающиеся множеств. На них универсальное множество изображают в виде прямоугольника, а его подмножества – кругами. Диаграммы, представленные на рис. 16.2.5 a) – d), иллюстрируют понятия, введенные выше.
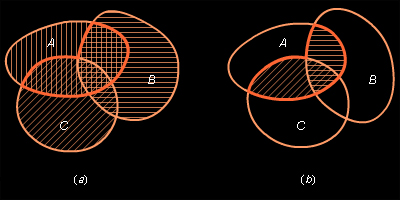
Диаграммами Эйлера–Венна удобно пользоваться для наглядного изображения между различными понятиями. На рисунке 16.2.5 a) и b) представлены отношения и – соответственно.
На рисунке 16.2.5 f) представлена диаграммама Эйлера–Венна для иллюстрации утверждения: если и то
Рисунок 16.2.5 g) можно рассматривать как иллюстрацию опроверждения утверждения: если и то
| Лучшие специалисты узи в Чебоксарах |
| лучшие узи чебоксары |
| lecardo.ru |
А также: библиотека ЭОРов и образовательный онлайн-сервис с тысячами интерактивных работ "Облако знаний".