
Учебник. Площадь круга
Площадь круга равна половине произведения длины ограничивающей ее окружности на радиус:
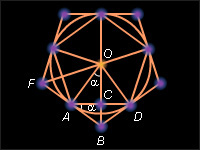
Построим два правильных n-угольника: P1 – вписанный в круг и P2 – описанный около круга (рис. 13.3.1).
Многоугольники являются простыми фигурами. Многоугольник содержит круг, а многоугольник содержится в круге. Радиусы, проведенные в вершины многоугольника разбивают его на n треугольников, равных треугольнику AOD. Поэтому Так как где p – периметр многоугольника r – радиус круга. Аналогично находим площадь многоугольника : Итак, многоугольник содержащийся в круге, имеет площадь а многоугольник, содержащий круг, имеет площадь При достаточно большом n периметр p отличается сколь угодно мало от длины l окружности, а cos α сколь угодно мало отличается от единицы, поэтому площади многоугольников сколь угодно мало отличаются от величины Согласно определению площади произвольной фигуры это значит, что площадь круга Теорема доказана.
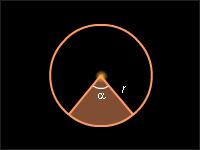
Площадь кругового сектора вычисляется по формуле где r – радиус круга, α – градусная мера соответствующего центрального угла (рис. 13.3.2).
|
|
|
||
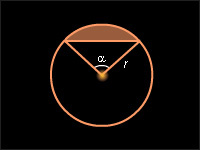
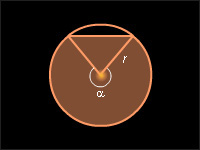
| Круговой сектор | Круговой сегмент | Круговой сегмент |
Площадь сегмента, не равного полукругу, вычисляется по формуле где α – градусная мера дуги кругового сегмента, а SΔ – площадь треугольника с вершинами в центре круга и концах радиусов, ограничивающих соответствующий сектор. Знак «–» выбирается, если α < 180° (рис. 13.3.3), знак «+», если α > 180° (рис. 13.3.4).
А также: библиотека ЭОРов и образовательный онлайн-сервис с тысячами интерактивных работ "Облако знаний".