
Учебник. Гомотетия
Гомотетией с центром O и коэффициентом k ≠ 0 называется преобразование, при котором каждой точке X ставится в соответствие точка так, что (см. рис. 12.6.1).
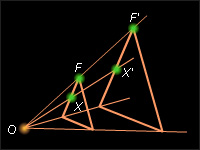
При гомотетии с коэффициентом k каждый вектор умножается на число k.
Пусть O – центр гомотетии, а точки A и B при гомотетии с коэффициентом k переходят в точки и Тогда Поэтому
Гомотетия с коэффициентом k является подобием с коэффициентом
По теореме 12.13 для любых двух точек A, B и их образов и при гомотетии верно, что Из этого равенства следует, что а это означает, что гомотетия с коэффициентом k является подобием с коэффициентом
Подобие с коэффициентом k есть композиция гомотетии с коэффициентом k и движения.
Пусть получена из фигуры F подобием с коэффициентом k (см. рисунок 12.6.2).
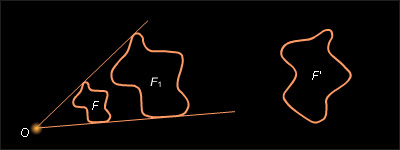
Гомотетией с коэффициентом k (и любым центром) переведем фигуру F в фигуру F1. Тогда любым точкам X, Y фигуры F ставят в соответствие такие точки X1, Y1, что X1Y1 = kXY. Но и для точек фигуры соответствующих точкам X, Y, также Поэтому Это равенство верно для любых точек , фигуры . Следовательно, фигуры и можно некоторым движением перевести в фигуру
Гомотетия отрезок переводит в отрезок.
Пусть гомотетия переводит концы отрезка AB в точки (см. рисунок 12.6.3).
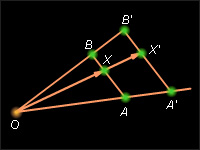
Точка X ∈ AB тогда и только тогда, когда где 0 ≤ λ ≤ 1 (см. теорему 10.4). При этом, если λ возрастает от 0 до 1, то X пробегает отрезок AB от A к B.
По свойству гомотетии и Из этих равенств Подставляя эти значения в равенство получим откуда А это равенство означает, что когда число λ возрастает от 0 до 1, точка пробегает отрезок
Гомотетия сохраняет величину угла.
Пусть A, B, C – заданные точки, а – их образы при гомотетии f с коэффициентом k. Пусть Тогда и (см. рис. 12.6.4).
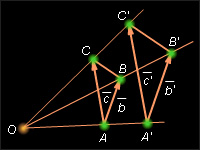
По основному свойству гомотетии Отсюда получаем, что Кроме того, Тогда Из равенства косинусов и следует равенство углов. Теорема доказана.
Гомотетия треугольник переводит в треугольник. Стороны этих треугольников пропорциональны, а соответственные углы равны.
Пусть дан треугольник ABC, и гомотетия переводит точки A, B, C в точки Тогда ΔABC переходит в так как отрезок AB переходит в отрезок AC – в BC – в Из теоремы 12.13 следует, что Отсюда и окончательно Равенство углов треугольника вытекает из теоремы 12.17. Теорема доказана.
- Подобие отрезок переводит в отрезок, прямую – в прямую, луч – в луч;
- Подобие сохраняет величину угла;
- Подобие переводит треугольник в треугольник. Соответственные стороны этих треугольников пропорциональны, а соответственные углы равны.
Композиция подобий с коэффициентами k1, k2 есть подобие с коэффициентами k1ċ k2.
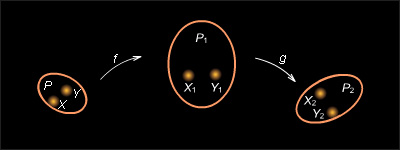
Пусть фигура P подобием f с коэффициентом k1 переводится в фигуру P1, а затем фигура P1 подобием g с коэффициентом k2 переводится в фигуру P2 (рис. 12.6.5).
Пусть точкам X, Y фигуры P соответствуют точки X1, Y1 фигуры P1. Тогда X1Y1 = kXY. Пусть далее точкам X1, Y1 фигуры P1 соответствуют точки X2, Y2 фигуры P2. Тогда X2Y2 = k2X1Y1. Тем самым точкам X, Y фигуры P соответствуют точки X2, Y2 фигуры P2, и из приведенных равенств следует, что X2Y2 = k1k2XY. В силу произвольности точек X и Y фигуры P это означает, что преобразование g ˆ f – подобие с коэффициентом k1k2.
А также: библиотека ЭОРов и образовательный онлайн-сервис с тысячами интерактивных работ "Облако знаний".