
Учебник. Параллельный перенос
Введем на плоскости систему координат O, X, Y. Преобразование фигуры F, при котором произвольная ее точка M (x; y) переходит в точку где a и b – одни и те же для всех точек (x; y), называется параллельным переносом. Параллельный перенос задается формулами (*) которые выражают координаты образа через координаты прообраза M при параллельном переносе.
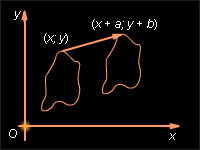
- При a = b = 0 параллельный перенос совпадает с тождественным преобразованием. При этом каждая точка плоскости – неподвижная точка преобразования;
- При a2 + b2 > 0 параллельный перенос не имеет неподвижных точек.
Каковы бы ни были две точки A и существует один и только один параллельный перенос, при котором точка A переходит в точку
Введем в плоскости систему координат OXY, и пусть
и
– заданные точки. Определим параллельный перенос f равенствами
где
Тогда данный параллельный перенос действительно переводит точку A в
так как
Параллельный перенос есть движение.
Действительно, две произвольные точки переходят при параллельном переносе в точки Поэтому Отсюда Таким образом, параллельный перенос сохраняет расстояние, а значит, является движением. Теорема доказана.
Движение, сохраняющее направление, является параллельным переносом.
Пусть f – движение, переводящее точку A в точку Пусть Выберем произвольную отличную от A точку B, и пусть По условию По теореме 12.8 имеем или, следовательно, Отсюда Ввиду произвольности выбора точки B теорема доказана.
А также: библиотека ЭОРов и образовательный онлайн-сервис с тысячами интерактивных работ "Облако знаний".