Учебник. Движение

Пусть X и Y – две разные точки, образы которых при преобразовании движения f совпадают, т. е. f (X) = f (Y). По определению ρ (f (X), f (Y)) = ρ (X, Y). С одной стороны, ρ (X, Y) ≠ 0, так как по условию X  ≠  Y. С другой стороны, ρ (f (X), f (Y)) = 0 в силу предположения. Полученное противоречие доказывает теорему.

Пусть f – заданное движение, $f^{\mathrm{ -}1}$  – обратное к нему преобразование, а $X^{\mathrm{ \prime }}$  и $Y^{\mathrm{ \prime }}$  – две точки плоскости, являющиеся образами точек X и Y. По определению обратного преобразования $f^{\mathrm{ -}1}\mathrm{,}$   при этом $X^{\mathrm{ \prime }}$   и $X^{\mathrm{ \prime }}\mathrm{.}$   Следовательно, $f^{\mathrm{ -}1}$  – движение. Теорема доказана.

Пусть движение переводит три точки A, B, C, лежащие на одной прямой, в точки $A^{\mathrm{ \prime }}$  соответственно, и для определенности положим, что точка B лежит между точками A и C. Тогда выполняются равенства $A^{\mathrm{ \prime }}\mathrm{.}$ Отсюда $A^{\mathrm{ \prime }}\mathrm{.}$   Это означает, что точка $B^{\mathrm{ \prime }}$   лежит между точками $A^{\mathrm{ \prime }}$   и $C^{\mathrm{ \prime }}\mathrm{.}$   Первая часть утверждения доказана.

Предположим, что найдутся три точки A, B, C, не лежащие на одной прямой, такие, что их образы $A^{\mathrm{ \prime }}$  при движении f лежат на некоторой прямой. Рассмотрим преобразование $f^{\mathrm{ -}1}\mathrm{.}$   По теореме 12.2 $f^{\mathrm{ -}1}$  – движение, и в соответствии с доказанным в первой части теоремы образы точек $A^{\mathrm{ \prime }}\mathrm{,}$  лежащих на одной прямой, также лежат на одной прямой. Но $f^{\mathrm{ -}1}\mathrm{,}$   а они по предположению не лежат на одной прямой. Полученное противоречие доказывает теорему.

1. Пусть концам отрезка AB движение f сопоставляет точки $A^{\mathrm{ \prime }}$  и $B^{\mathrm{ \prime }}\mathrm{.}$   Возьмем любую точку X отрезка AB. Тогда по теореме 12.3 $X^{\mathrm{ \prime }}$  лежит на прямой $A^{\mathrm{ \prime }}{B}^{\mathrm{ \prime }}$  между точками $A^{\mathrm{ \prime }}$  и $B^{\mathrm{ \prime }}\mathrm{,}$  то есть на отрезке $A^{\mathrm{ \prime }}{B}^{\mathrm{ \prime }}\mathrm{.}$  Наоборот, любую точку $Y^{\mathrm{ \prime }}$  отрезка $A^{\mathrm{ \prime }}{B}^{\mathrm{ \prime }}$  преобразование $f^{\mathrm{ -}1}$  преобразует в точку Y, принадлежащую отрезку AB, так как $f^{\mathrm{ -}1}$  – также движение. Теорема доказана.
2. Пусть A и B – произвольные точки данной прямой, $A^{\mathrm{ \prime }}$  – прямая, проведенная через образы точек A и B при движении f. Рассмотрим произвольную точку C прямой AB. По теореме 12.3 точки $A^{\mathrm{ \prime }}\mathrm{,}$  где $C^{\mathrm{ \prime }}\mathrm{,}$  лежат на одной прямой, т.е. прямой $A^{\mathrm{ \prime }}\mathrm{.}$  Аналогично в силу того, что $f^{\mathrm{ -}1}$  – движение, для точки $D^{\mathrm{ \prime }}$  прямой $A^{\mathrm{ \prime }}$  существует точка D прямой AB такая, что $D^{\mathrm{ \prime }}\mathrm{.}$  Поскольку при движении взаимное расположение точек сохраняется, то луч переходит в луч при преобразовании движения.
3. По теореме 12.3 три точки A, B, C, не лежащие на одной прямой, переходят при преобразовании движения в точки $A^{\mathrm{ \prime }}$  соответственно, не лежащие на одной прямой. Кроме того, отрезки AB, BC и AC переходят в отрезки $A^{\mathrm{ \prime }}\mathrm{.}$  Таким образом, треугольник ABC переходит в треугольник $A^{\mathrm{ \prime }}\mathrm{.}$   Причем по определению движения $A^{\mathrm{ \prime }}\mathrm{.}$   Тогда по третьему признаку равенства треугольников треугольники ABC и $A^{\mathrm{ \prime }}$  равны.

Рассмотрим три точки A, B, C, не лежащие на одной прямой. Они задают лучи AB и AC, являющиеся сторонами угла BAC. Пусть $A^{\mathrm{ \prime }}$  – соответственно образы рассматриваемых точек A, B, C. Докажем, что $\mathrm{\angle }\mathrm{.}$   Согласно доказательству предыдущей теоремы треугольник ABC равен треугольнику $A^{\mathrm{ \prime }}\mathrm{,}$  а из равенства треугольников следует, что $\mathrm{\angle }\mathrm{.}$  Теорема доказана.

К теореме 12.5

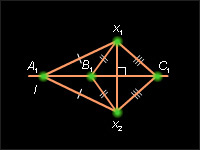
Возьмем любую точку X ∈ F. Пусть X₁ = f (X) и X₂ = g (X). Покажем, что X₁ и X₂ совпадают. Допустим, что X₁ и X₂ – различные точки. Так как f и g – движения, то X₁A₁ = XA и X₂A₁ = XA. Поэтому A₁X₂ = A₂X₂, т.е. точка A₁ равноудалена от точек X₁ и X₂. Следовательно, точка A₁ лежит на серединном перпендикуляре отрезка X₁X₂ – прямой l (см. рис. 12.2.1).

Но точно также можно сказать, что и точки B₁ и C₁ лежат на одной прямой l. Мы получим, что точки A₁, B₁, C₁ лежат на одной прямой l. Это противоречит теореме 12.3. Итак, $X_1$   и $X_2$   совпадают, и в силу произвольности выбора X движения f и g совпадают.

Введем векторы $\stackrel{⟶}{u}\mathrm{.}$   В силу равенства треугольников ABC и $A_1{B}_1{C}_1$ имеем равенства ${\left(\stackrel{⟶}{A_1{B}_1}\right)}^2\mathrm{,}$ т.е. ${\left(\stackrel{⟶}{u_1}\right)}^2\mathrm{.}$   (*) Пусть P – любая точка. Разложим вектор $\stackrel{⟶}{AP}$   по векторам $\stackrel{⟶}{AB}$   и $\stackrel{⟶}{AC}\mathrm{.}$   Получим $\stackrel{⟶}{AP}\mathrm{.}$   Зададим преобразование f следующим образом: каждой точке P поставим в соответствие точку $P$ так, что если $\stackrel{⟶}{AP}\mathrm{,}$   то $\stackrel{⟶}{A_1{P}_1}\mathrm{.}$   Для этого преобразования $f(A)=A_1$ т.к. при P = A α = β = 0, что дает $P_1=A_1$  $f(B)=B_1$ т.к. при P = B α = 1, β = 0, тогда $P_1=B_1$ И, наконец, $f(C)=C_1$ Докажем, что f – движение. Возьмем любые две точки P и Q и соответствующие им точки $P_1=f(P)$ и $Q_1=f(Q)$ Пусть $\stackrel{⟶}{AP}\mathrm{,}$   $\stackrel{⟶}{AQ}\mathrm{.}$   Тогда $\stackrel{⟶}{A_1{P}_1}\mathrm{,}$   $\stackrel{⟶}{A_1{Q}_1}$   и $\stackrel{⟶}{PQ}\mathrm{,}$   $\stackrel{⟶}{P_1{Q}_1}\mathrm{.}$   Возведя в скалярный квадрат эти равенства, получим ${\stackrel{⟶}{PQ}}^2$ и ${\stackrel{⟶}{P_1{Q}_1}}^2\mathrm{.}$ Ввиду равенств (*) имеем ${\stackrel{⟶}{PQ}}^2\mathrm{,}$   или $PQ=P_1{Q}_1$ Следовательно, f – движение. Теорема доказана.