
Учебник. Векторные уравнения прямой
Положение прямой на плоскости может быть задано одним из следующих способов:
- прямая l проходит через точку параллельно вектору
- прямая l проходит через точки и
- прямая l проходит через точку перпендикулярно вектору
- прямая l проходит через точку и составляет с вектором угол α (см. рис. 11.5.1).
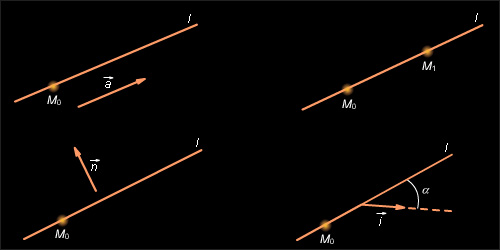
Любой вектор параллельный прямой l, называется направляющим вектором этой прямой. Любой вектор перпендикулярный прямой l, называется нормальным вектором прямой. Если взять на прямой какие-либо две фиксированные точки и то вектор в частности, будет направляющим вектором прямой
Пусть прямая l задана точкой и направляющим вектором (см. рис. 11.5.2). Пусть M – произвольная точка прямой.
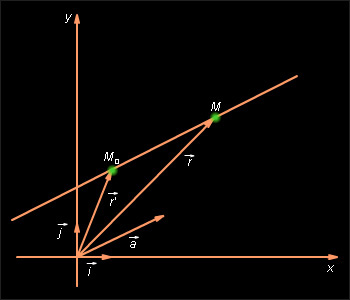
|
|
Обозначим
и
радиус-векторы точек
и M соответственно. Вектор
параллелен прямой, и, следовательно, вектору
тогда и только тогда, когда M лежит на прямой. Так как
то
Если ввести систему координат
то уравнение можно записать в виде
Пусть и тогда из уравнений следует, что и, окончательно, уравнение которое называется каноническим уравнением прямой, с направляющим вектором
Если
то параметрическое уравнение примет вид
Это уравнение задает прямую, параллельную оси Oy и проходящую через точку
Каноническое уравнение прямой имеет вид
Аналогично, если
то прямая, задаваемая системой
Как было отмечено ранее, направляющим вектором прямой можно выбрать вектор
где
и
– произвольные две точки прямой. Тогда, подставив координаты вектора
в каноническое уравнение, получим уравнение прямой, проходящей через две заданные точки:
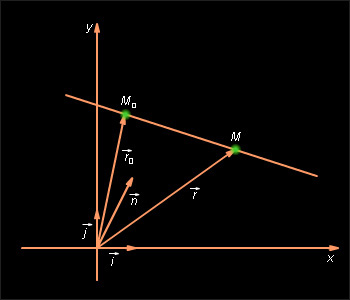
Пусть
– некоторая точка прямой,
– вектор, перпендикулярный прямой, а
– произвольная точка этой прямой (см. рис. 11.5.3). Тогда M лежит на прямой тогда и только тогда, когда вектор
перпендикулярен вектору
а для этого необходимо и достаточно, чтобы скалярное произведение векторов
и
равнялось нулю:
Введя радиус-векторы
и
точек
и M, это уравнение можно записать в виде
Это – нормальное векторное уравнение прямой, а
– нормальный вектор прямой. Если переписать его через координаты точек
M и вектор
в ортогональной декартовой системе координат, получим
В § 11.4 было показано, что любая прямая может быть задана этим уравнением при условии Назовем это уравнение общим уравнением прямой. Следовательно, для любой прямой, заданной общим уравнением Ax + By + C = 0, можно считать, что вектор перпендикулярен прямой, а вектор параллелен ей. Действительно, так как векторы и взаимно ортогональны, а поскольку – нормальный вектор к прямой, то параллелен ей. Тогда – направляющий вектор прямой.
При рассмотрении векторно-параметрического уравнения прямой мы показали, как перейти к каноническому уравнению, из которого легко получить общее уравнение прямой. Аналогично, из нормального векторного уравнения так же легко перейти к общему уравнению прямой. Покажем теперь, как из общего уравнения прямой получить ее векторные уравнения.
Пусть прямая задана общим уравнением Ax + By + C = 0 в прямоугольной декартовой системе координат. Тогда мы знаем, что вектор
– направляющий вектор прямой,
– ее нормальный вектор. Так как
предположим для определенности, что A ≠ 0. Тогда точка
принадлежит прямой. В этом легко убедиться, подставив координаты точки в уравнение прямой. Приведенных данных достаточно, чтобы получить векторные уравнения прямой. Действительно,
А также: библиотека ЭОРов и образовательный онлайн-сервис с тысячами интерактивных работ "Облако знаний".