Открытая Математика. Планиметия. Эллипс и его свойства

Эллипс и его свойства

В § 7 было получено уравнение фигуры, которую мы назвали эллипсом: $\frac{x^{2}}{b^{2}} + \frac{{(y - \frac{1 + k^{2}}{1 - k^{2}} \frac{p}{2})}^{2}}{a^{2}} = 1, k < 1 .$ Перейдем в новую систему координат, перенеся начало системы координат в точку $O' (0; \frac{1 + k^{2}}{1 - k^{2}} \frac{p}{2})$ и повернув оси исходной системы на угол 90°.

В соответствии с формулами преобразования координат выразим старые координаты через новые по формулам: ${\begin{array}{l} x = x' cos 90^{ˆ} - y' sin 90^{ˆ}, \\ y = \frac{1 + k^{2}}{1 - k^{2}} \frac{p}{2} + x' sin 90^{ˆ} + y' cos 90^{ˆ}, \end{array}$ или ${\begin{array}{l} x = - y', \\ y = x' + \frac{1 + k^{2}}{1 - k^{2}} \frac{p}{2} . \end{array}$ В новой системе координат, которую называют канонической, уравнение эллипса имеет вид $\frac{{x'}^{2}}{a^{2}} + \frac{{y'}^{2}}{b^{2}} = 1,$ при этом $\frac{b^{2}}{a^{2}} = \frac{k^{2} p^{2}}{1 - k^{2}} \frac{{(1 - k^{2})}^{2}}{k^{2} p^{2}} = 1 - k^{2} < 1,$ то есть при k < 1 получим, что a > b > 0. В дальнейшем для удобства будем опускать знак "штрих" и будем вместо x' (y') писать x (y). Таким образом, получим уравнение эллипса в новой системе координат. $\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1, a > b > 0 .$ Это уравнение называется каноническим уравнением эллипса.

Рассмотрим свойства эллипса.

Эллипс пересекает каждую из осей координат в двух точках.

Для определения точек пересечения эллипса с осью Ox нужно решить совместно два уравнения $\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1 и y = 0 .$ Отсюда получим x = ±a. Таким образом, точками пересечения эллипса с осью Ox будут точки A (a; 0) и C (–a; 0).

Аналогично, точки пересечения эллипса с осью Oy – B (0; b) и D (0; –b).

Точки A, B, C и D называются вершинами эллипса. Отрезок AC называется большой осью эллипса, отрезок BD – малой осью. Числа a и b называют полуосями эллипса. Точки $F_{1} (- c; 0)$ и $F_{2} (c; 0),$ где $c = \sqrt{a^{2} - b^{2}},$ называются фокусами эллипса.

Пусть M (x; y) – произвольная точка эллипса. Найдем расстояния от точки M до фокусов эллипса. $F_{1} M = \sqrt{{(x + c)}^{2} + y^{2}};$ $F_{2} M = \sqrt{{(x - c)}^{2} + y^{2}} .$ Рассмотрим выражение ${(x \pm c)}^{2} + y^{2} = x^{2} \pm 2 x c + c^{2} + y^{2} = x^{2} \pm 2 x c + a^{2} - b^{2} + y^{2} =$
$= x^{2} \pm 2 x c + a^{2} - b^{2} + b^{2} (1 - \frac{x^{2}}{a^{2}}) = \frac{a^{2} - b^{2}}{a^{2}} x^{2} \pm 2 x c + a^{2} = \frac{c^{2}}{a^{2}} x^{2} \pm 2 x \frac{c}{a} a + a^{2} = {(a + \frac{c}{a} x)}^{2} .$ Здесь мы учли, что координаты (x; y) точки M удовлетворяют уравнению эллипса.

Величину $ε = \frac{c}{a}$ называют эксцентриситетом эллипса. Очевидно, для эллипса ε < 1. Поскольку $| x | \leq a,$ то отсюда следует, что a – εx > 0. Поэтому $F_{1} M = a + ε x;$ $F_{2} M = a - ε x .$

Сумма расстояний от любой точки эллипса до его фокусов есть величина постоянная и равная удвоенной большей полуоси.

Действительно, используя полученные выражения для расстояний от точки эллипса до его фокусов, получим $F_{1} M + F_{2} M = a + ε x + a - ε x = 2 a .$

Эллипс имеет две взаимно перпендикулярные оси симметрии.

В уравнение эллипса переменные x и y входят только во второй степени, поэтому если точка $M (x; y)$ принадлежит эллипсу, то точки $M_{1} (x; - y)$ и $M_{2} (- x; y)$ также принадлежат ему, так как их координаты удовлетворяют уравнению эллипса. Точка $M_{1}$ симметрична точке M относительно оси Ox, а точка $M_{2}$ – относительно Oy. Таким образом, эллипс имеет две оси симметрии, они взаимно перпендикулярны. Большая и малая полуоси эллипса лежат на его осях симметрии.

Эллипс имеет центр симметрии.

Если координаты точки M (x; y) удовлетворяют уравнению эллипса, то этому же уравнению удовлетворяют и координаты точки N (–x; –y). Точка M симметрична точке N относительно начала координат. Таким образом, эллипс имеет центр симметрии.

Центр симметрии эллипса называется центром эллипса.

Эллипс может быть получен сжатием окружности.

Пусть $ω (0, a)$ – окружность с центром в начале координат и радиуса a. Тогда $\frac{X^{2}}{a^{2}} + \frac{Y^{2}}{a^{2}} = 1 .$ Точке $P (X; Y)$ на окружности сопоставим точку $P_{1} (x; y)$ такую, что $x = X и y = \frac{b}{a} Y .$ Точка $P_{1}$ получается сдвигом точки P, при котором абцисса не меняется, а ордината уменьшается в отношении $\frac{b}{a} .$ Координаты точки $P_{1}$ удовлетворяют уравнению эллипса. В самом деле, $\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = \frac{X^{2}}{a^{2}} + \frac{{(\frac{b}{a} Y)}^{2}}{b^{2}} = \frac{X^{2}}{a^{2}} + \frac{Y^{2}}{b^{2}} = 1 .$

Таким образом, эллипс можно получить из окружности равномерным сжатием к оси Ox, при котором ординаты точек уменьшаются в одном и том же соотношении, равном $\frac{b}{a} .$ Отсюда следует, что форма эллипса зависит от значения отношения $\frac{b}{a} :$ чем меньше это отношение, тем более сжатым будет эллипс, и наоборот, чем больше отношение $\frac{b}{a},$ тем эллипс будет менее сжатым.

В качестве характеристики формы эллипса удобнее пользоваться эксцентриситетом. Так как $ε = \frac{c}{a} = \frac{\sqrt{a^{2} - b^{2}}}{a} = \sqrt{1 - {(\frac{b}{a})}^{2}},$ то чем больше ε, тем более сжат эллипс.

При малых значениях эксцентриситета эллипс мало отличается от окружности. При ε = 0 эллипс превращается в окружность.

В § 7 мы определили эллипс как множество точек, отношение расстояний от которых до данной точки A и данной прямой l есть величина постоянная и равная числу k.

Рассмотрим, какие координаты имеет точка A и какое уравнение – прямая l в канонической системе координат. Для начала отметим, что в силу введенных ранее обозначений $\frac{b^{2}}{a^{2}} = \frac{k^{2} p^{2}}{1 - k^{2}} \frac{{(1 - k^{2})}^{2}}{k^{2} p^{2}} = 1 - k^{2} .$ Тогда $ε = \sqrt{1 - {(\frac{b}{a})}^{2}} = \sqrt{1 - (1 - k^{2})} = k .$ Таким образом, данное в условии исходной задачи число, характеризующее величину отношения расстояний от точки эллипса до точки A и прямой l, есть эксцентриситет эллипса.

Координаты точки $A (0; \frac{p}{2})$ при переходе в новую систему будут равны: ${\begin{array}{l} x' = \frac{p}{2} - \frac{1 + k^{2}}{1 - k^{2}} \frac{p}{2} = - \frac{k^{2} p}{1 - k^{2}} = - a ε = - c \\ y' = - x = 0 \end{array} .$ То есть точка A в новой системе координат имеет те же координаты, что и фокус $F$ эллипса и поэтому совпадет с ним.

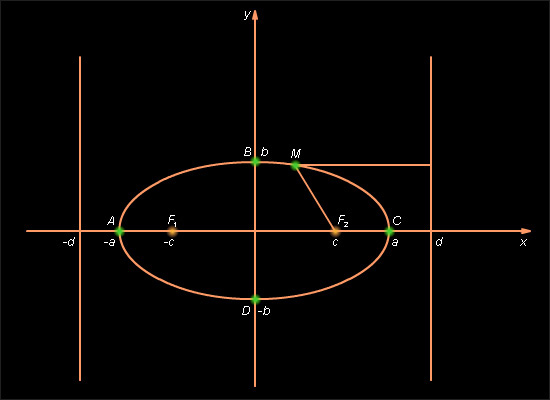
Уравнение прямой в исходной системе координат имело вид $y = - \frac{p}{2} .$ После замены системы координат получим новое уравнение прямой l $x' = - \frac{p}{2} - \frac{1 + k^{2}}{1 - k^{2}} \frac{p}{2} = \frac{- p}{1 - k^{2}} .$ Обозначим $\frac{p}{1 - k^{2}} = d$ и покажем, что $d = \frac{a}{ε} .$ Действительно, $\frac{a}{ε} = \frac{p k}{(1 - k^{2}) ε} = \frac{p k}{(1 - k^{2}) k} = \frac{p}{(1 - k^{2})} = d .$ Поскольку для эллипса ε < 1, то $d = \frac{a}{ε} > a .$

Прямая x = –d называется директрисой, соответствующей фокусу F₁(-c; 0). Наряду с этой директрисой вводят прямую x = d, которая является директрисой, соответствующей фокусу F₂(c; 0).

С учетом свойств симметрии эллипса, свойство, с помощью которого мы определили эллипс, в новых терминах можно сформулировать следующим образом: отношение расстояния от любой точки эллипса до одного из его фокусов к расстоянию от этой точки до соответствующей ему директрисы есть величина постоянная и равная эксцентриситету. Вид эллипса в канонической системе координат и его директрисы приведены на рис. 10.8.1.

Смотрите также: Математика, Английский язык, Химия, Биология, Физика, География, Астрономия.
А также: библиотека ЭОРов и образовательный онлайн-сервис с тысячами интерактивных работ "Облако знаний".

Учебник. Эллипс и его свойства

ГЛАВНАЯ

НОВОСТИ

УЧЕБНИК

ДОСТУП К БЕСПЛАТНЫМ УРОКАМ