 |
 |
Среди плоских многоугольников особое место занимают правильные многоугольники. Как известно, для любого натурального
Еще в древней Греции были известны пять удивительных многогранников.
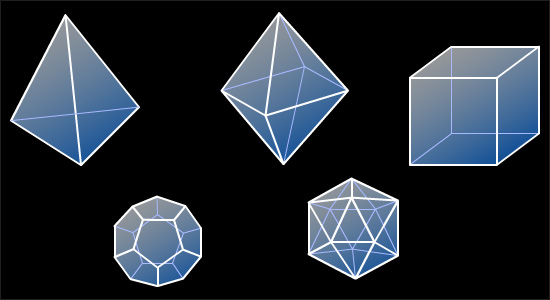
|
| Рисунок 8.1.1 |
Их изучали ученые, ювелиры, священники, архитекторы. Этим многогранникам даже приписывали магические свойства. Древнегреческий ученый и философ Платон (IV–V в до н. э.) считал, что эти тела олицетворяют сущность природы. В своем диалоге «Тимей» Платон говорит, что атом огня имеет вид тетраэдра, земли – гексаэдра (куба), воздуха – октаэдра, воды – икосаэдра. В этом соответствии не нашлось места только додекаэдру и Платон предположил существование еще одной, пятой сущности – эфира, атомы которого как раз и имеют форму додекаэдра. Ученики Платона продолжили его дело в изучении перечисленных тел. Поэтому эти многогранники называют платоновыми телами.

Многогранник называется правильным, если все его грани – равные между собой правильные многоугольники, из каждой его вершины выходит одинаковое число ребер и все двугранные углы равны.
Оказывается, что существует всего пять видов правильных многогранников. Докажем это, а затем предъявим каждый из них, доказав тем самым их существование.

Рассмотрим многогранный угол с вершиной

Существует не более пяти различных видов правильных многогранников.
Заметим, что из этой теоремы не следует, что существует именно пять видов правильных многогранников. Теорема лишь утверждает, что таких видов не более пяти, а теперь нам осталось доказать, что этих видов действительно пять, предъявив все пять видов многогранников.
 |
 |
 |

