 |
 |

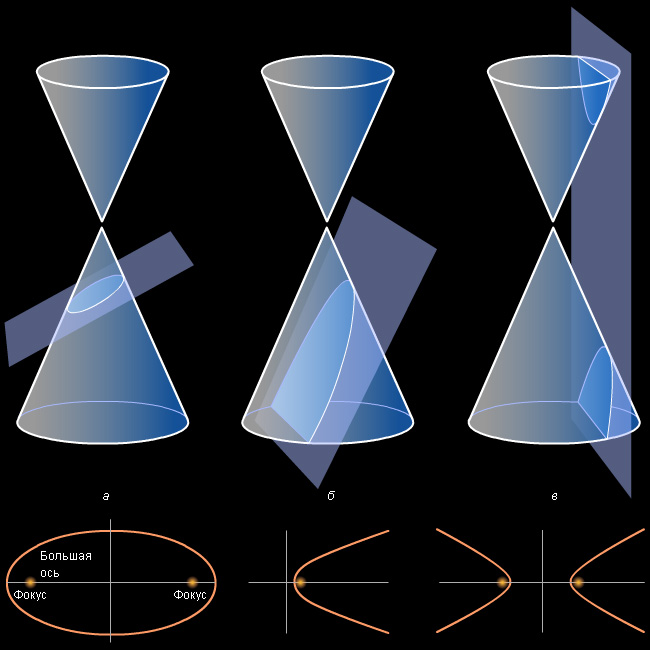
Конические сечения – плоские кривые, которые получаются пересечением прямого кругового конуса плоскостью.
За исключением вырожденных случаев, коническими сечениями являются эллипсы, гиперболы или параболы. С точки зрения аналитической геометрии коническое сечение представляет собой геометрическое место точек, удовлетворяющих уравнению второго порядка.
Открывателем конических сечений предположительно считается Менехм (IV в. до н. э.). Менехм использовал параболу и равнобочную гиперболу для решения задачи об удвоении куба.
Трактаты о конических сечениях, написанные Аристеем и Евклидом в конце IV в. до н. э., были утеряны, но материалы из них вошли в знаменитые «Конические сечения» Аполлония Пергского, которые сохранились до нашего времени. Аполлоний, варьируя угол наклона секущей плоскости, получил все конические сечения из одного кругового конуса, прямого или наклонного. Аполлонию мы обязаны и современными названиями кривых – эллипс, парабола и гипербола.
В своих построениях Аполлоний использовал двуполостной круговой конус, поэтому впервые стало ясно, что гипербола – кривая с двумя ветвями. Со времен Аполлония конические сечения делятся на три типа в зависимости от наклона секущей плоскости к образующей конуса. Эллипс образуется, когда секущая плоскость пересекает все образующие конуса в точках одной его полости; парабола – когда секущая плоскость параллельна одной из касательных плоскостей конуса; гипербола – когда секущая плоскость пересекает обе полости конуса.
|
| Рисунок 5.3.1 |
Изучая конические сечения как пересечения плоскостей и конусов, древнегреческие математики рассматривали их и как траектории точек на плоскости.
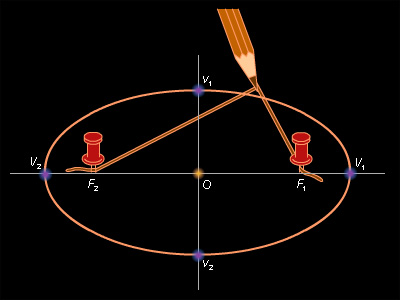
Эллипс можно определить как геометрическое место точек, сумма расстояний от которых до двух заданных точек постоянна; параболу – как геометрическое место точек, равноудаленных от заданной точки и заданной прямой; гиперболу – как геометрическое место точек, разность расстояний от которых до двух заданных точек постоянна.
Эти определения конических сечений как плоских кривых подсказывают и способ их построения с помощью натянутой нити.
Эллипс. Если концы нити заданной длины закреплены в точках
|
| Рисунок 5.3.2 |
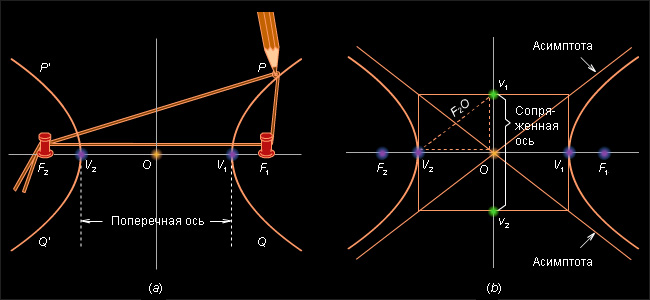
Гипербола. При построении гиперболы точка  мы вычерчиваем, предварительно поменяв шпеньки
мы вычерчиваем, предварительно поменяв шпеньки
|
| Рисунок 5.3.3 |
Ветви гиперболы приближаются к двум прямым, которые пересекаются между ветвями. Эти прямые, называемые асимптотами гиперболы, строятся как показано на рисунке 5.3.3, б. Угловые коэффициенты этих прямых равны
 где
где 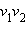 – отрезок биссектрисы угла между асимптотами, перпендикулярной отрезку
– отрезок биссектрисы угла между асимптотами, перпендикулярной отрезку
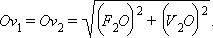 |
Если асимптоты гиперболы взаимно перпендикулярны, то гипербола называется равнобочной. Две гиперболы, имеющие общие асимптоты, но с переставленными поперечной и сопряженной осями, называются взаимно сопряженными.
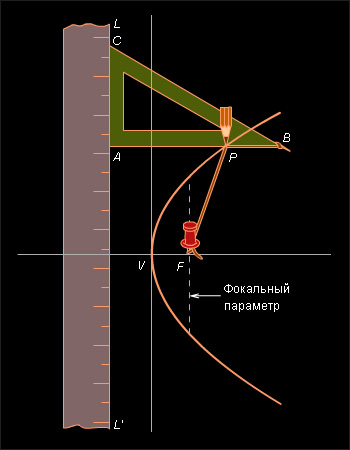
Парабола. Фокусы эллипса и гиперболы были известны еще Аполлонию, но фокус параболы, по-видимому, впервые установил Папп (вторая пол. III в.), определивший эту кривую как геометрическое место точек, равноудаленных от заданной точки (фокуса) и заданной прямой, которая называется директрисой. Построение параболы с помощью натянутой нити, основанное на определении Паппа, было предложено Исидором Милетским (VI в.).
|
| Рисунок 5.3.4 |
Расположим линейку так, чтобы ее край совпал с директрисой
 (рис. 5.3.4), и приложим к этому краю катет
(рис. 5.3.4), и приложим к этому краю катет 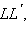 так как общая длина нити равна
так как общая длина нити равна
Заметим, что существуют и вырожденные случаи конических сечений. Они появляются в тех случаях, когда секущая плоскость проходит через вершину конуса. Если наклон плоскости к оси конуса больше, чем наклон образующей к оси, то сечением является точка – вершина конуса. Если эти углы совпадают, то есть секущая плоскость касается конуса, то коническим сечением будет одна прямая. Наконец, в случае, когда угол наклона секущей плоскости меньше, она пересекает конус по двум прямым.

|
| Рисунок 5.3.5 |
 |
 |
 |

