Задачи с решениями

Изображаем прямой параллелепипед ABCDA₁B₁C₁D₁ и производим маркировку рисунка. ABCD – ромб. Значит, AB = AD = a. Угол DAB острый. По условию 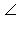DAB = α (0° < α < 90°). O – центр ромба ABCD.

Рассмотрим треугольник ABO. Диагонали ромба взаимно перпендикулярны, поэтому 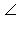AOB = 90°. Тогда (поскольку диагональ ромба является биссектрисой его угла,   Заметим, что поскольку угол α острый. Значит, 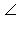ABO >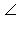OAB. В треугольнике против большого угла лежит большая сторона, значит, AO > BO и AC > BD. Таким образом, мы выяснили, что AC – большая диагональ ромба ABCD. Но тогда A₁C – большая диагональ данного параллелепипеда. Заканчивая маркировку рисунка, заметим, что по условию 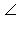ACA₁ = γ (0° < γ < 90°).

Известно, что S_п = 2S₀ + S_б, где S_п – площадь полной поверхности параллелепипеда, S₀ – площадь основания, S_б – площадь боковой поверхности.

Вынесем основание параллелепипеда во фронтальную плоскость. Из прямоугольного ΔABO находим, что Тогда Из прямоугольного ΔACA₁ находим: (высота параллелепипеда).

Зная формулу площади ромба, находим: S₀ = a²sin α. Известно, что S_б = PH, где P – периметр основания. В данном случае P = 4a, поэтому
Подставляя полученные значения в формулу (1), имеем

Ответ: