4.4. Трехгранный угол

Определение 4.5.

Трехгранный угол – это часть пространства, ограниченная тремя плоскими углами с общей вершиной и попарно общими сторонами, не лежащими в одной плоскости (чертеж 4.4.1). Общая вершина О этих углов называется вершиной трехгранного угла. Стороны углов называются ребрами, плоские углы при вершине трехгранного угла называются его гранями. Грани трехгранного угла образуют двугранные углы.

Чертеж 4.4.1

Теорема 4.2. Неравенство треугольника для трехгранного угла.

Каждый плоский угол трехгранного угла меньше суммы двух других его плоских углов.

Теорема 4.3.

α + γ + β < 360°. Другими словами, сумма плоских углов трехгранного угла меньше 360°.

Теорема 4.4. Теорема косинусов для трехгранного угла.

cos α = cos β cos γ + sin β sin γ cos A,

где α, β, γ – плоские углы, A – двугранный угол, составленный плоскостями углов β и γ.

Замечание. С помощью доказанной теоремы можно вычислить величину двугранного угла, зная плоские углы трехгранного угла:

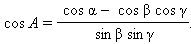Если грани плоских углов взаимно перпендикулярны, получаем формулу трех косинусов: cos α = cos β cos γ.

Теорема 4.5. Теорема синусов для трехгранного угла.

Справедливо равенство

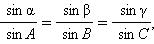где α, β, γ – плоские углы трехгранного угла; A, B, C – противолежащие им двугранные углы.

Определение 4.6.

Несколько плоских углов с общим началом O, из которых никакие два не лежат в одной плоскости, образуют многогранный угол (чертеж 4.4.5). Эти плоские углы при вершине многогранного угла называются гранями, а стороны этих углов – ребрами, точка O – вершиной многогранного угла. По числу граней многогранный угол называется трехгранным, четырехгранным и т.д. Если все грани многогранного угла находятся с одной стороны от каждой из плоскостей его граней, угол называется выпуклым. В данном курсе рассматриваются только выпуклые многогранные углы.

Теорема 4.6.

Каждый плоский угол многогранного угла меньше суммы всех остальных его плоских углов.

Глава 4. Многогранники

4.4. Трехгранный угол window.top.document.title = "4.4. Трехгранный угол";

4.4. Трехгранный угол