Глава 16. Введение в математическую логику
16.2. Отношения между множествами
Пусть во множестве A задано некоторое отношение "○".
Определение 16.4.
Отношение "○" рефлексивно, если для любого элемента a из множества A выполнено a○a (т.е. любой элемент связан отношением ○ с самим собой).
Например: отношение равенства на множестве отрезков рефлексивно, так как любой отрезок равен сам себе.
Определение 16.5.
Отношение ○ симметрично, если из a○b следует b○a для любых элементов a и b множества A. Отношение равенства на множестве отрезков является симметричным, так как если [AB] = [CD], то и [CD] = [AB].
Определение 16.6.
Отношение ○ называется транзитивным, если из того, что a○b и b○c следует, что a○c.
В частности, отношение равенства отрезков рефлексивно, так как если отрезок AB равен отрезку CD, а отрезок CD равен отрезку MN, то отрезок AB равен отрезку MN.
Определение 16.7.
Отношение ○ во множестве A называется отношением эквивалентности, если оно одновременно рефлексивно, симметрично и транзитивно.
Всякое отношение эквивалентности  во множестве A позволяет специальным образом различать элементы этого множества. Обозначим через C (a) множество всех элементов x из A, таких, что
во множестве A позволяет специальным образом различать элементы этого множества. Обозначим через C (a) множество всех элементов x из A, таких, что  Это множество является подмножеством A, которое называется классом эквивалентности a. Если
Это множество является подмножеством A, которое называется классом эквивалентности a. Если  то в силу симметричности и транзитивности отношения
то в силу симметричности и транзитивности отношения  любой элемент x, эквивалентный a, эквивалентен и b. Если же b не эквивалентен a, то C (a) и C (b) не имеют общих элементов, потому что если
любой элемент x, эквивалентный a, эквивалентен и b. Если же b не эквивалентен a, то C (a) и C (b) не имеют общих элементов, потому что если  и
и  , то в силу симметричности
, то в силу симметричности  и
и  , и в силу транзитивности
, и в силу транзитивности  что противоречит условию. Таким образом, отношением эквивалентности множество A разбивается на непересекающиеся классы эквивалентности, при котором каждый элемент A попадает в свой класс.
что противоречит условию. Таким образом, отношением эквивалентности множество A разбивается на непересекающиеся классы эквивалентности, при котором каждый элемент A попадает в свой класс.
Как мы видели в приведенных выше примерах, равенство на множестве отрезков является отношением эквивалентности и задает его разбиение на классы эквивалентности. Каждый такой класс содержит отрезки заданной длины.
Например: если две прямые a и b не пересекаются, то можно записать a b =
b = 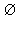 , если же они пересекаются, то по определению их пересечением является общая точка A (a
, если же они пересекаются, то по определению их пересечением является общая точка A (a b = A). Пересечением луча a с дополняющим его лучом a' является их общее начало O (a
b = A). Пересечением луча a с дополняющим его лучом a' является их общее начало O (a a' = O).
a' = O).
Определение 16.9. Объединением двух множеств A и B называется множество, состоящее из тех элементов, которые принадлежат хотя бы одному из этих множеств. Обозначение: A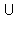 B, где символ
B, где символ 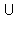 – знак объединения множеств.
– знак объединения множеств.
Например: объединением луча a с дополняющим его лучом a' является прямая.
Определение 16.10. Разностью двух множеств A и B называется такое множество, в которое входят все те элементы, которые принадлежат A и не принадлежат B. Обозначение: A \ B. Если B – подмножество A, то A \ B называют дополнением к B и обозначают B'.
Например: разностью прямой a и ее луча с началом O является множество точек дополняющего луча a' без начальной точки O.
Введенные операции обладают рядом свойств.
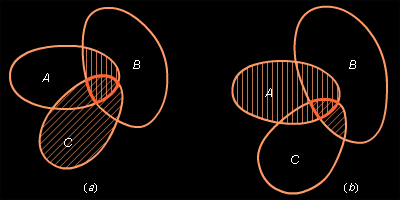
Пусть x (A (A B) B) C, отсюда x C, отсюда x (A (A B) и x B) и x C, или x C, или x A, x A, x B, x B, x C. Отсюда x C. Отсюда x (B (B C) и x C) и x A, следовательно, x A, следовательно, x A A (B (B C) и верно (A C) и верно (A B) B) C C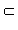 A A (B (B C). Наоборот, если x C). Наоборот, если x A A (B (B C), следует, что x C), следует, что x A, x A, x C, x C, x B, откуда x B, откуда x (A (A B) B) C и верно A C и верно A (B (B C) C)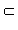 (A (A B) B) C. Отсюда A C. Отсюда A (B (B C) = (A C) = (A B) B) C (см. рис. 16.2.1 a), b)). Аналогично доказывается равенство множеств A C (см. рис. 16.2.1 a), b)). Аналогично доказывается равенство множеств A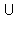 (B (B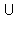 C) = (A C) = (A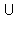 B) B) C. C.
 1
|
| Рисунок 16.2.1
|
|
Пусть x A A B, то есть x B, то есть x A и x A и x B, отсюда x B, отсюда x A. Пусть теперь x A. Пусть теперь x A. Из условия A A. Из условия A B следует, что x B следует, что x B, отсюда x B, отсюда x A A B. Следовательно, A B. Следовательно, A B = A. B = A.
Пусть x A A B, тогда x B, тогда x A или x A или x B. Но A B. Но A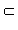 B, и, следовательно, x B, и, следовательно, x B, A B, A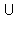 B B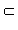 B. Если x B. Если x B, то по определению x B, то по определению x A A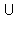 B и верно включение B B и верно включение B A A B. Отсюда A B. Отсюда A B = B (см. рис. 16.2.2). B = B (см. рис. 16.2.2).
 2
|
| Рисунок 16.2.2
|
|
Связь операций пересечения и объединения множеств отражает свойство дистрибутивности.
Понятия множества и подмножества используются при определении многих понятий математики и, в частности, при определении геометрической фигуры.
Определим как универсальное множество плоскость. Тогда можно дать следующее определение геометрической фигуры в планиметрии.
Определение 16.11. Геометрической фигурой называется всякое множество точек плоскости.
Таким образом, как сама точка, так и конечное и бесконечное множество точек являются геометрическими фигурами.
Из определения 16.11 непосредственно следует, что объединение и пересечение геометрических фигур есть геометрическая фигура.
Если фигура F1 явлется собственным подмножеством фигуры F2, то говорят также, что F1 – часть фигуры F2. Например, отрезок AB – часть прямой.
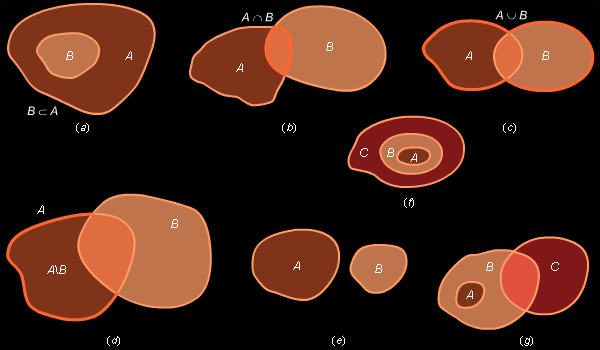
Чтобы наглядно отображать множества и отношения между ними, рисуют геометрические фигуры, которые находятся между собой в этих отношениях. Такие изображения множеств называют диаграммами Эйлера–Венна. Диаграммы Эйлера–Венна делают наглядными различные утверждения, касающиеся множеств. На них универсальное множество изображают в виде прямоугольника, а его подмножества – кругами. Диаграммы, представленные на рис. 16.2.5 a) – d), иллюстрируют понятия, введенные выше.
 5
|
| Рисунок 16.2.5
|
Диаграммами Эйлера–Венна удобно пользоваться для наглядного изображения между различными понятиями. На рисунке 16.2.5 a) и b) представлены отношения  и
и  – соответственно.
– соответственно.
На рисунке 16.2.5 f) представлена диаграммама Эйлера–Венна для иллюстрации утверждения: если  и
и  то
то 
Рисунок 16.2.5 g) можно рассматривать как иллюстрацию опроверждения утверждения: если  и
и  то
то 


Смотрите также:
Математика,
Английский язык,
Химия,
Биология,
Физика,
География,
Астрономия.
А также:
библиотека ЭОРов и образовательный онлайн-сервис с тысячами интерактивных работ
"Облако знаний".






 во множестве
во множестве  Это множество является подмножеством
Это множество является подмножеством  то в силу симметричности и транзитивности отношения
то в силу симметричности и транзитивности отношения  любой элемент
любой элемент  и
и  , то в силу симметричности
, то в силу симметричности  и
и  , и в силу транзитивности
, и в силу транзитивности  что противоречит условию. Таким образом, отношением эквивалентности множество
что противоречит условию. Таким образом, отношением эквивалентности множество 
![]() B
B![]()
![]() B ≠
B ≠ ![]()
![]() B =
B = ![]()
![]() b =
b = ![]()
![]() b = A)
b = A)![]() a' = O)
a' = O)
![]() B
B![]()

![]() B = B
B = B![]() A; A
A; A![]() B = B
B = B![]() A
A![]() B
B![]() B = A
B = A![]() B = B
B = B![]() (B
(B![]() C) = (A
C) = (A![]() B)
B)![]() (A
(A![]() C)
C)![]() (B
(B![]() C) = (A
C) = (A![]() B)
B)![]() (A
(A![]() C)
C)

 и
и  – соответственно.
– соответственно.
 и
и  то
то 
 и
и  то
то 




