Найдите объем цилиндра, имеющего наибольший объем среди всех цилиндров, вписанных в сферу радиуса R.
Решение.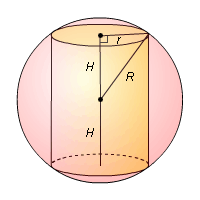
1
Радиус основания цилиндра
r, высота цилиндра
2H и радиус сферы
R связаны теоремой Пифагора:
Объем цилиндра равен
Условие максимума:
т.е.
Убеждаемся, что это максимум: производная меняет знак с «+» на «–». Искомый объем равен
function showUserAnswer(){
testSolution='
Смотрите также:
Математика,
Английский язык,
Химия,
Биология,
Физика,
География,
Астрономия.
А также:
библиотека ЭОРов и образовательный онлайн-сервис с тысячами интерактивных работ
"Облако знаний".
Задачи
6 из 6
