Числовую последовательность, все члены которой отличны от нуля и каждый член которой, начиная со второго, получается из предыдущего члена умножением его на одно и то же число q, называют геометрической прогрессией, а число q – знаменателем этой прогрессии. По определению, геометрическая прогрессия задается рекуррентно формулой
b1 = b, bn = bn – 1 ∙ q.
Для n-го члена последовательности справедливо равенство
bn = b1qn – 1.
Верна также формула
Сумма n членов геометрической прогрессии определяется формулой
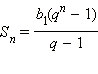(при q ≠ 1).
В интерактивном режиме вы можете ввести значения первого члена и знаменателя геометрической прогрессии. Программа покажет формулы для нахождения n-го члена прогрессии и суммы n членов. Введя номер n члена прогрессии, можно найти численные значения этих величин. Чтобы перейти в демонстрационный режим, щёлкните по кнопке с кинопроектором. Нажмите кнопку Старт, чтобы начать анимацию, Стоп – чтобы приостановить её и Сброс – чтобы вернуть анимацию в исходное состояние. Для возвращения в интерактивный режим нажмите на кнопку с изображением руки.
Модель 1.18.
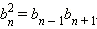
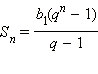(при 
