Глава 3. Решение уравнений и неравенств
3.2.
3.2.1.
Понятно, что a, являясь решением неравенства (1), может лежать только в ОДЗ.
Поскольку проверить решение в неравенствах не так просто, как в уравнениях, искать решения лучше сразу в ОДЗ.
Решить неравенство − это означает найти все его решения или доказать, что их нет. Совокупность всех решений неравенства называется множеством решений неравенства.
Два неравенства,
называются равносильными на множестве X, если на этом множестве неравенства имеют одни и те же решения, то есть, если каждое решение неравенства (2) является решением неравенства (3), и наоборот, каждое решение второго неравенства является решением первого. Два неравенства, не имеющие решений на каком-либо множестве, также считаются равносильными на этом множестве.
Из приведённого определения следует, что если неравенство f1 (x) < g1 (x) окажется более простым, чем равносильное ему неравенство f (x) < g (x), то и решать нужно именно его, так как решения у него те же. Остаётся единственная проблема: как от неравенства (2) перейти к равносильному ему неравенству (3) или, как говорят, осуществить равносильный переход? Сформулируем несколько общих правил, позволяющих это делать.
Правило 1. Если функции f (x), g (x) и h (x) определены на множестве X, то неравенства
| f (x) > g (x) и f (x) + h (x) > g (x) + h (x) |
равносильны на этом множестве.
Правило 2. Если h (x) > 0 на множестве X, то неравенства
равносильны на этом множестве.
Вывод. Обе части неравенства можно умножать на положительную функцию, не нарушая равносильности.
Правило 3. Если h (x) < 0 на множестве X, то неравенства
равносильны на этом множестве.
Вывод. Обе части неравенства можно умножать на отрицательную функцию, не нарушая равносильности, меняя при этом знак неравенства на противоположный.
Правило 4. Если f (x) ≥ 0, g (x) ≥ 0 на множестве X, то неравенства
равносильны на этом множестве.
Вывод. Если обе части неравенства 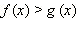 неотрицательны, то возведение в квадрат неравенства не нарушает равносильности. Заметим, что возводить неравенство в квадрат можно, только если обе части этого неравенства неотрицательны. Если хотя бы одна из частей неравенства отрицательна, возведение неравенства в квадрат, вообще говоря, не является равносильным преобразованием. Яснее всего это видно на примере числовых неравенств. Так, если верное неравенство −1 > −4 возвести в квадрат, то получится неверное неравенство 1 > 16. Такое противоречие вызвано именно тем, что части первоначального неравенства не были неотрицательными.
неотрицательны, то возведение в квадрат неравенства не нарушает равносильности. Заметим, что возводить неравенство в квадрат можно, только если обе части этого неравенства неотрицательны. Если хотя бы одна из частей неравенства отрицательна, возведение неравенства в квадрат, вообще говоря, не является равносильным преобразованием. Яснее всего это видно на примере числовых неравенств. Так, если верное неравенство −1 > −4 возвести в квадрат, то получится неверное неравенство 1 > 16. Такое противоречие вызвано именно тем, что части первоначального неравенства не были неотрицательными.
Пример 1Равносильны ли неравенства 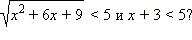
Неравенства неравносильны. Действительно,
Неравенство x + 3 < 5 будет верным и тогда, когда x + 3 < –5, например, при x = –100. Первое же неравенство при x = –100 неверно.
Ответ. Нет.
|
Пример 2Равносильны ли неравенства 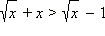 и
и 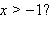
Неравенства неравносильны. В самом деле,
Значит, множеством решений первого неравенства являются область x ≥ 0, а второго x > –1. Поскольку это разные множества, то неравенства неравносильны.
Ответ. Нет.
|


Смотрите также:
Математика,
Английский язык,
Химия,
Биология,
Физика,
География,
Астрономия.
А также:
библиотека ЭОРов и образовательный онлайн-сервис с тысячами интерактивных работ
"Облако знаний".














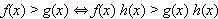
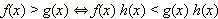
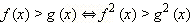
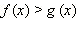 неотрицательны, то возведение в квадрат неравенства не нарушает равносильности. Заметим, что возводить неравенство в квадрат можно, только если обе части этого неравенства неотрицательны. Если хотя бы одна из частей неравенства отрицательна, возведение неравенства в квадрат, вообще говоря, не является равносильным преобразованием. Яснее всего это видно на примере числовых неравенств. Так, если верное неравенство −1 > −4 возвести в квадрат, то получится неверное неравенство 1 > 16. Такое противоречие вызвано именно тем, что части первоначального неравенства не были неотрицательными.
неотрицательны, то возведение в квадрат неравенства не нарушает равносильности. Заметим, что возводить неравенство в квадрат можно, только если обе части этого неравенства неотрицательны. Если хотя бы одна из частей неравенства отрицательна, возведение неравенства в квадрат, вообще говоря, не является равносильным преобразованием. Яснее всего это видно на примере числовых неравенств. Так, если верное неравенство −1 > −4 возвести в квадрат, то получится неверное неравенство 1 > 16. Такое противоречие вызвано именно тем, что части первоначального неравенства не были неотрицательными.



