 |
 |
Можно еще больше расширить числовое множество – так, чтобы операция деления над натуральными числами была выполнима всегда. Для этого введем понятие дроби.
 |
 |
|
 |
 |
|
Если 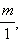 и её часто записывают просто
и её часто записывают просто
 |
 |
|
 |
 |
|
Например, 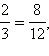 так как
так как 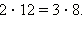 Из этого определения следует, что дробь
Из этого определения следует, что дробь 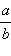 равна любой дроби вида
равна любой дроби вида 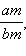 где
где 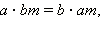 то
то 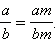 Итак, мы готовы сформулировать следующее правило.
Итак, мы готовы сформулировать следующее правило.
| Основное свойство дроби Если числитель и знаменатель данной дроби умножить или разделить на одно и то же число, неравное нулю, то получится дробь, равная данной. |
С помощью основного свойства дроби можно заменить данную дробь другой дробью, равной данной, но с меньшими числителем и знаменателем. Такая замена называется сокращением дроби. Например, 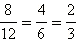 (здесь числитель и знаменатель разделили сначала на 2, а потом ещё на 2). Сокращение дроби можно провести тогда и только тогда, когда её числитель и знаменатель не являются взаимно простыми числами. Если же числитель и знаменатель данной дроби взаимно просты, то дробь сократить нельзя, например,
(здесь числитель и знаменатель разделили сначала на 2, а потом ещё на 2). Сокращение дроби можно провести тогда и только тогда, когда её числитель и знаменатель не являются взаимно простыми числами. Если же числитель и знаменатель данной дроби взаимно просты, то дробь сократить нельзя, например, 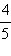 – несократимая дробь.
– несократимая дробь.

 |
|
Модель 1.5.
Сокращение обыкновенных дробей
|
 |
 |
|
 |
 |
|
Справедливо следующее утверждение (его мы докажем ниже):
Всякую неправильную дробь можно представить в виде суммы натурального числа и правильной дроби. |
Из двух дробей с одинаковыми знаменателями больше та дробь, числитель которой больше. Например, 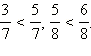 Из двух дробей с одинаковыми числителями больше та дробь, знаменатель которой меньше. Например,
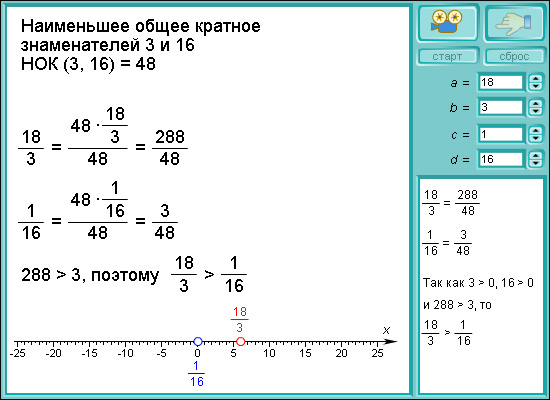
Из двух дробей с одинаковыми числителями больше та дробь, знаменатель которой меньше. Например, 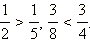 Чтобы сравнить две дроби с разными числителями и знаменателями, нужно преобразовать обе дроби так, чтобы их знаменатели стали одинаковыми. Такое преобразование называется приведением дробей к общему знаменателю.
Чтобы сравнить две дроби с разными числителями и знаменателями, нужно преобразовать обе дроби так, чтобы их знаменатели стали одинаковыми. Такое преобразование называется приведением дробей к общему знаменателю.

 |
|
Модель 1.6.
Сравнение обыкновенных дробей
|
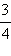 и
и 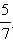 Умножим числитель и знаменатель первой дроби на 7, получим
Умножим числитель и знаменатель первой дроби на 7, получим 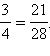 Умножим числитель и знаменатель второй дроби на 4, получим
Умножим числитель и знаменатель второй дроби на 4, получим 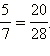 Итак, две дроби
Итак, две дроби 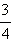 и
и 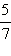 приведены к общему знаменателю:
приведены к общему знаменателю:
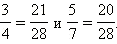 |
Теперь знаменатели этих дробей одинаковы, значит, 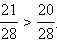 Следовательно,
Следовательно, 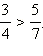 Ясно, что две дроби можно привести не к единственному общему знаменателю. Так, в нашем примере дроби
Ясно, что две дроби можно привести не к единственному общему знаменателю. Так, в нашем примере дроби 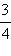 и
и 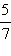 можно привести к знаменателю 56. В самом деле:
можно привести к знаменателю 56. В самом деле:
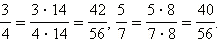 |
Привести дроби к наименьшему общему знаменателю: 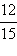 и
и 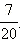
|
Найдём сперва наименьшее общее кратное чисел 15 и 20. НОК (15, 20) = 60. Так как 60 : 15 = 4, то числитель и знаменатель дроби
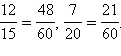
|
В рассмотренном примере числа 4 и 3 называют дополнительными множителями для первой и второй дроби соответственно.
Теперь мы можем определить арифметические действия с дробями.
Сложение. Если знаменатели дробей одинаковы, то чтобы сложить эти дроби, нужно сложить их числители; знаменатель остаётся прежним, то есть
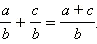 |
Вычитание. Если две дроби имеют одинаковые знаменатели, то
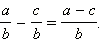 |

 |
|
Модель 1.7.
Сложение и вычитание обыкновенных дробей
|
Умножение. Произведение двух дробей равно дроби, числитель которой равен произведению числителей данных дробей, а знаменатель равен произведению их знаменателей, то есть
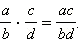 |
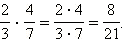
Деление. Деление дробей осуществляют следующим образом:
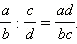 |
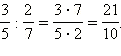
В случае умножения и деления смешанных чисел всегда удобно переходить к неправильным дробям.

 |
|
Модель 1.8.
Умножение и деление обыкновенных дробей
|
Теперь можно показать, что любую неправильную дробь можно представить в виде суммы натурального числа и правильной дроби (или в виде натурального числа, если дробь 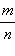 такова, что число
такова, что число 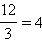 ).
).
Представить неправильную дробь в виде суммы натурального числа и правильной дроби: 1) 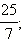 2)
2) 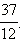
Всякую неправильную дробь можно представить в виде смешанного числа (или в виде натурального числа). Понятно также, что верно и обратное: всякое смешанное число может быть представлено в виде неправильной дроби. Например, 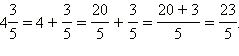
 |
 |
 |

